Proving g(x) is continuous over interval (-∞,-2)

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For number 18,

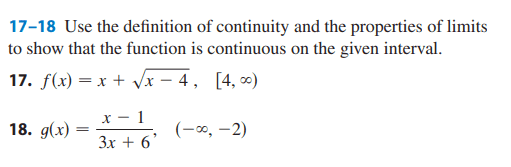
The solution is,

However, should they not write "For $-∞ < a < -2$" since $a ≠ -∞$ (infinity is not a number)?

Many thanks!

 

[Office_Shredder]

$a$ is a number, so can't be negative infinity.

In particular, $a\in [-\infty,-2)$ isn't really a meaningful thing outside of people abusing notation.

 

[member 731016]

$a$ is a number, so can't be negative infinity.

In particular, $a\in [-\infty,-2)$ isn't really a meaningful thing outside of people abusing notation.

Thank you for your reply @Office_Shredder !

So a better notation than $a < -2$ is $-∞ < a < -2$, correct?

Many thanks!

 

[Office_Shredder]

Thank you for your reply @Office_Shredder !

So a better notation than $a < -2$ is $-∞ < a < -2$, correct?

Many thanks!

No, the $-\infty<a$ notation conveys no additional information. $a$ and $a>-\infty$ are the same thing. You can include the negative infinity, but in no sense is it better here.

 

[Mark44]

However, should they not write "For −∞<a<−2"

$-\infty < a < -2$ and $a \in (-\infty, -2)$ are two different notations that say exactly the same thing. In most of the books I've seen, interval notation, as in the 2nd example above, uses a parenthesis to indicate an endpoint that isn't included, and a bracket to indicate that an endpoint is included. I've seen other notations used, but these seem to be a lot rarer.

Also, I don't think any textbook would include "For" in a compound inequality. $-\infty < a < -2$ says everything that needs to be said.

 

[member 731016]

Thank for your help @Office_Shredder and @Mark44!