Question about the property of PDF

[songoku]

Homework Statement

Please see below

Relevant Equations

P(X = a) = $\int_{a}^{a} f(x) dx = 0$

Derivative of CDF = PDF

This is part of my note:

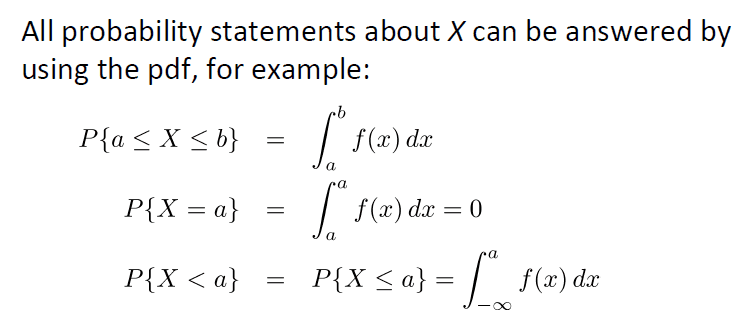
Now, this is practice question:

I want to ask why P(X = 2) is not zero, because from the note: P{X = a} = $\int_{a}^{a} f(x) dx=0$ ?

If I differentiate F(x), I will get f(x) which is the pdf, then using the pdf to find P(X = 2), I think I will get zero as the probability.

Thanks

 

[BvU]

Hi,

there is something fundamentally wrong with your relevant equation: the right hand side is zero !
(as you discovered )

Probability density $f$ is defined such that $f(x) \, \bf dx$ is the probability to find something in an interval [x, x+dx]

Since the probability to find something somewhere is 1, PDFs tend to be normalized:$$\int_{-\infty}^\infty f(x) \,dx = 1 $$ and that's what should help you find the answer...

[edit] adapt notation $f$ for probability density

$\$

 

[BvU]

If I differentiate F(x)

Have you been introduced to the properties of the Dirac delta function ?

I must confess the given information : P(2) = 1/2 is highly confusing. You sure it's not F(2) = 1/2 ?

[edit] but that conflicts with $F$ given for $x\ge 2$ - - - is there an error in the problem statement ?

Advice: assume a value for $a$, use the fact that $F(+\infty)=1$ and sketch $F$ and $P$.

$\$

 

[songoku]

Hi,

there is something fundamentally wrong with your relevant equation: the right hand side is zero !
(as you discovered )

Do you mean the formula I wrote in "relevant equation" is wrong?

P(X = a) = $\int^{a}_{a} f(x) dx=0$ is not correct?

Have you been introduced to the properties of the Dirac delta function ?

No, I have not been introduced to that terrifying function

I must confess the given information : P(2) = 1/2 is highly confusing. You sure it's not F(2) = 1/2 ?

What I post is the exact question and up until this moment there is no revision to the question

I am not sure whether the question is somewhat similar or related to this one:
https://www.physicsforums.com/threa...e-distribution-function.1056469/#post-6957692

I can do the question in that thread but now I think about it, why P(X ≤ i) and P(X < i) is not the same and why P(X = i) is not zero? Because from the note, P(X < a) = P(X ≤ a) = $\int_{-\infty}^{a} f(x) dx$

Thanks

 

[Steve4Physics]

I’m no expert but a couple of thoughts...

The given CDF consists of 3 'steps'. That means we are dealing with a system with 3 discrete ‘allowed states’ at $x=-1$, $x=1$ and $x=2$ such that:
$f(x=-1) = p$
$f(x=1) = q$
$f(x=2) = r$
where $p+q+r=1$.
Otherwise $f(x) = 0$.

EDIT
I suspect (like @BvU) that there is a mistake in the question. If $P(X=2) =1/2$ should actually be $f(x=2) = 1/2$, the question is then easily answered (only simple algebra/arithmetic needed).

 

[BvU]

Do you mean the formula I wrote in "relevant equation" is wrong?

P(X = a) = $\int^{a}_{a} f(x) dx=0$ is not correct?

It is correct, but then what can we say about the given $P(X=2)={1\over 2}$ ? When the relevant equation clearly states $P(X=z) = 0$ for any $z$ ?

No, I have not been introduced to that terrifying function

Then the other thread is also a mystery to you ? Or do you understand that your PDF is the sum of three delta functions with different 'amplitude' ?

What I post is the exact question and up until this moment there is no revision to the question

Fair enough,, but that doesn't guarantee that there is no mistake ...

Advice: assume a value for a, use the fact that F(+∞)=1 and sketch F and P.

I am not sure whether the question is somewhat similar or related to this one:
https://www.physicsforums.com/threa...e-distribution-function.1056469/#post-6957692

I can do the question in that thread but now I think about it, why P(X ≤ i) and P(X < i) is not the same and why P(X = i) is not zero? Because from the note, P(X < a) = P(X ≤ a) = $\int_{-\infty}^{a} f(x) dx$

Thanks

Seems to me that one is still open too ...

 

[pbuk]

Derivative of CDF = PDF

Fine, but what happens when the CDF cannot be differentiated?

I want to ask why P(X = 2) is not zero

Because P(X=2) is given in the question and is 0.5.

because from the note: P{X = a} = $\int_{a}^{a} f(x) dx=0$ ?

Because the note only applies where the CDF is differentiable (and where the PDF is integrable). The CDF in the question clearly has a step discontinuity at $x=2$.

$f(x=-1) = p$
$f(x=1) = q$
$f(x=2) = r$
where $p+q+r=1$.
Otherwise $f(x) = 0$.

Looks good to me.

I suspect (like @BvU) that there is a mistake in the question. If $P(X=2) =1/2$ should actually be $f(x=2) = 1/2$, the question is easily answered (only simple algebra/arithmetic needed).

I don't see a mistake - why do you think $P(X=2)$ can't be $\frac 1 2$?

 

[Steve4Physics]

I don't see a mistake - why do you think $P(X=2)$ can't be $\frac 1 2$?

There is no problem with $P(X=2)= \frac 12$.

I messed up. I thought that the equation $P(X=a) = \int_a^a f(x) dx = 0$ (in Post #1) was part of the question. But it is not part of the question and isn’t relevant here (as we are not dealing with a continuous probability distribution).

EDITED

 

[songoku]

Fine, but what happens when the CDF cannot be differentiated?

Because the note only applies where the CDF is differentiable (and where the PDF is integrable). The CDF in the question clearly has a step discontinuity at $x=2$.

Ahh I see, so that's my mistake.

Then the other thread is also a mystery to you ? Or do you understand that your PDF is the sum of three delta functions with different 'amplitude' ?

Not a mystery anymore (but I still don't understand about delta function and have not learned about it)

Thank you very much for all the help and explanation BvU, Steve4Physics, pbuk