Questions concerning the geometry of spacetime

[student34]

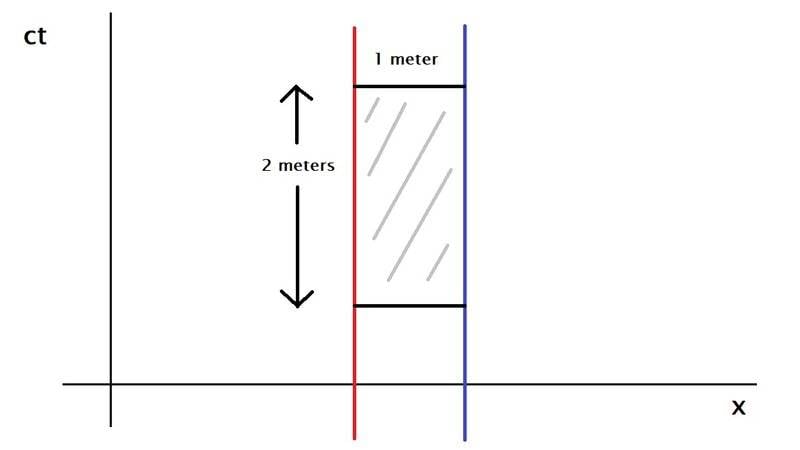
I have some questions about the space of the rectangle shown in the spacetime diagram. The red and blue lines are world lines of objects at rest with each other.

1) Does the rectangle have an area? (if no please go to question 3)

2) Is the rectangle a 2d Euclidean space? (if no please go to question 4)

3) If 1 is no, is there a geometrical way to explain how something with 4 sides can connect at the corners, have distinct lengths and still not have an area?

4) If 2 is no, is there a geometrical way to explain how something with 4 sides can connect at the corners, have distinct lengths, exist in only 2 dimensions (I put this in italics because I am not sure if we can't have higher dimensions to hold the 2d objects in relativity) and still not be a 2d Euclidean space?

 

[PeterDonis]

1) Does the rectangle have an area? (if no please go to question 3)

It has a "spacetime area", but that's not the same as an ordinary area.

2) Is the rectangle a 2d Euclidean space?

No.

3) If 1 is no, is there a geometrical way to explain how something with 4 sides can connect at the corners, have distinct lengths and still not have an area?

Your statement here is based on a false assumption, that the only kind of "area" possible is an ordinary area. That's wrong. As above, the rectangle has a "spacetime area"--it has two timelike sides and two spacelike sides. There are geometrical rules about how such things work, but they're spacetime geometrical rules, not ordinary Euclidean geometrical rules.

In short, you have failed to consider the fact that Euclidean geometry is not the only possible geometry.

4) If 2 is no, is there a geometrical way to explain how something with 4 sides can connect at the corners, have distinct lengths, exist in only 2 dimensions (I put this in italics because I am not sure if we can't have higher dimensions to hold the 2d objects in relativity) and still not be a 2d Euclidean space?

Because, as just noted, Euclidean geometry is not the only possible kind of geometry. The 2D space in the spacetime diagram has Minkowskian geometry.

 

[FactChecker]

Your concept of "area" should be expanded to the general concept of an object "area" in two dimensions, whether those dimensions are physical space, time, or other abstract dimensions. The generalized concept of "area" still has great value and utility. There are transformations that are "area preserving" even though none of its dimensions are physical space.
The same can be said for three-dimensional and higher-dimensional "volume". There are useful concepts a general 2-dimensional "area" being cross-multiplied (or outer multiplied) by another dimension to give a 3-dimensional "volume".

 

[student34]

It has a "spacetime area", but that's not the same as an ordinary area.

Yes, that is what I have been told. But what troubles me is that we are only talking about 2 dimensions. How can there be so much mystery, especially since all 4 sides are connected in 2 dimensions. I would like to know exactly what makes this area so strange and so special.

 

[student34]

Your concept of "area" should be expanded to the general concept of an object "area" in two dimensions, whether those dimensions are physical space, time, or other abstract dimensions. The generalized concept of "area" still has great value and utility. There are transformations that are "area preserving" even though none of its dimensions are physical space.
The same can be said for three-dimensional and higher-dimensional "volume". There are useful concepts a general 2-dimensional "area" being cross-multiplied (or outer multiplied) by another dimension to give a 3-dimensional "volume".

I am not sure that I understand what you are getting at. I guess I am interested to know the properties that the temporal dimension has that other dimension don't have. And what can we say about the rectangle that can make visual sense to humans? For example, if we can't say that the rectangle has a 2d Euclidean area, can we say that it has a perimeter?

 

[Dale]

How can there be so much mystery

Statements like this are not helpful, it just encourages people to waste effort in addressing your opinion rather than the actual physics that you are struggling with

The particular “area” that you drew is not particularly useful. However, @robphy has some really great material using spacetime rectangles that are bounded on all sides by light pulses. These have a useful property that the “area” formed that way is invariant.

 

[PeterDonis]

what troubles me is that we are only talking about 2 dimensions.

Sure, because you only used 2 of the 4 spacetime dimensions when you drew your diagram. Just as many people draw diagrams of ordinary Euclidean space on a sheet of paper.

How can there be so much mystery

Mystery about what? There is no mystery whatever about how Minkowskian geometry works, in either 2 or 4 dimensions.

I would like to know exactly what makes this area so strange and so special.

As compared to what? To an ordinary rectangle in Euclidean space? Why would you not expect the rectangle you drew in spacetime to be different?

I guess I am interested to know the properties that the temporal dimension has that other dimension don't have.

We measure arc lengths along a timelike dimension using clocks. We measure arc lengths along a spacelike dimension using rulers. That is the physical difference between the two. Mathematically, timelike squared intervals have opposite sign in the metric to spacelike squared intervals.

 

[PeterDonis]

These have a useful property that the “area” formed that way is invariant.

The area formed by the rectangle the OP drew is also invariant under Lorentz transformations; it's just that in a different frame it won't look like a rectangle, it will look like a parallelogram. But that's also true of the areas with lightlike sides that appear in @robphy's diagrams: Lorentz transformations change the shape of those too (to be a more or less elongated rhombus), while preserving their area.

In fact, Lorentz transformations in a given 2-dimensional spacetime plane (more precisely, Lorentz boosts in a plane with one timelike and one spacelike dimension) preserve the area (as computed by the Minkowski metric) of any 2-dimensional figure in that plane.

 

[student34]

Statements like this are not helpful, it just encourages people to waste effort in addressing your opinion rather than the actual physics that you are struggling with

I have no other way to describe it other than this dimension is very very mysterious to me, it fascinates me to no end. It seems just as strange to me if not more strange than something like quantum mechanics.

The particular “area” that you drew is not particularly useful. However, @robphy has some really great material using spacetime rectangles that are bounded on all sides by light pulses. These have a useful property that the “area” formed that way is invariant.

It's interesting to think of invariant rectangles made that way. I looked but did not find any material on @robphy 's profile.

I hope to understand as much as I can about this rectangle in a practical sense.

 

[student34]

Sure, because you only used 2 of the 4 spacetime dimensions when you drew your diagram. Just as many people draw diagrams of ordinary Euclidean space on a sheet of paper.

Wouldn't the extra spatial dimensions just make my illustration needlessly more complicated? I am trying to focus on the properties of the temporal dimension and the properties of the relationship between the temporal dimension and the spatial dimension.

As compared to what? To an ordinary rectangle in Euclidean space? Why would you not expect the rectangle you drew in spacetime to be different?

From what I understand, the world lines are straight and we know that the horizontal measurements are straight. And all 4 sides are connected in a 2d space. How does this not have to be a 2d Euclidean rectangle that I am describing?

We measure arc lengths along a timelike dimension using clocks. We measure arc lengths along a spacelike dimension using rulers. That is the physical difference between the two. Mathematically, timelike squared intervals have opposite sign in the metric to spacelike squared intervals.

But that just seems like an extrinsic difference between the two different dimensions. In other words, we are just measuring length in a different way.

 

[Dale]

I have no other way to describe it other than this dimension is very very mysterious to me

It doesn’t matter if you have no other way or not. Such descriptions are unhelpful. They don’t identify any specific conceptual hurdle, they are not responsive to anything anyone else has said. They contribute nothing to advancing the conversation, and they detract from the scientific discussion.

Please stick to productive comments. If a comment is unproductive then just don’t say it.

 

[Dale]

I am trying to focus on the properties of the temporal dimension and the properties of the relationship between the temporal dimension and the spatial dimension.

There are only two properties of the temporal dimension that distinguish it from the spatial dimensions:

1) there is only one temporal dimension
2) it has a different sign in the signature

Everything else stems from those two features.

 

[PeterDonis]

Wouldn't the extra spatial dimensions just make my illustration needlessly more complicated?

You don't have to convince me that you don't need the extra spatial dimensions for the basic idea you are exploring. But you might need to convince yourself, since you said:

what troubles me is that we are only talking about 2 dimensions.

Why should this trouble you if adding more dimensions just makes things needlessly more complicated?

From what I understand, the world lines are straight

For the scenario we are discussing, yes.

and we know that the horizontal measurements are straight.

For the scenario we are discussing, yes.

And all 4 sides are connected in a 2d space.

Yes, but not a 2d Euclidean space; a 2d Minkowskian space.

How does this not have to be a 2d Euclidean rectangle that I am describing?

I've already told you: because Euclidean geometry is not the only possible geometry. The 2d "space" (or more precisely spacetime) that we are discussing here has Minkowskian geometry, not Euclidean geometry. That's just a physical fact. We know it's a physical fact because to properly model what happens in relativity, we need to use Minkowskian geometry; Euclidean geometry simply does not give the right answers.

But that just seems like an extrinsic difference between the two different dimensions. In other words, we are just measuring length in a different way.

So you think what a clock measures and what a ruler measures are the same thing? Why? Isn't it just obvious that these are physically different measurements of physically different things?

 

[robphy]

It's interesting to think of invariant rectangles made that way. I looked but did not find any material on @robphy 's profile.

It’s in my signature that is at the bottom of my posts… but maybe they don’t always show up.

https://www.physicsforums.com/insights/spacetime-diagrams-light-clocks/

https://www.physicsforums.com/insights/relativity-rotated-graph-paper/

https://www.physicsforums.com/insights/relativity-on-rotated-graph-paper-a-graphical-motivation/

from

https://www.physicsforums.com/insights/author/robphy/

 

[robphy]

The area formed by the rectangle the OP drew is also invariant under Lorentz transformations; it's just that in a different frame it won't look like a rectangle, it will look like a parallelogram. But that's also true of the areas with lightlike sides that appear in @robphy's diagrams: Lorentz transformations change the shape of those too (to be a more or less elongated rhombus), while preserving their area.

The key feature of the light-clock diamonds" and "causal diamonds"
(compared to other areas one might use in the spacetime plane) is that the edges are along the light-cone.

• The size of the diamond-area (as well as any area in the spacetime plane) is preserved because
  the determinant of the boost equals 1 (the product of the eigenvalues equals 1). [This is associated with the relativity-principle.]
  The area is equal to the square-interval.
• The directions of the diamond-edges are preserved because of the lightlike directions are eigenvectors.
  [This is associated with the speed-of-light-principle.]

(That is to say, we are working in an eigenbasis of the boost.)

Another feature is that the diamonds are traced out by the light-signals in a longitudinal light-clock (not the more common transverse light-clock found in typical textbooks).

Related to this is that all observers will choose the same events (not merely the same size of the area)
in constructing a given diamond,
since it is the future of the lower vertex intersected with the past of the upper vertex.

On top of all this, I worked out an efficient method of calculation
which is based on the Bondi k-calculus,
which is algebraically simpler and
arguably more physical and more relativistic in spirit (in the spirit of Minkowski),
compared to the standard textbook treatment of moving boxcars in space [not spacetime] and formulas in rectangular coordinates (in the spirit of Einstein).

 

[FactChecker]

I am not sure that I understand what you are getting at. I guess I am interested to know the properties that the temporal dimension has that other dimension don't have. And what can we say about the rectangle that can make visual sense to humans? For example, if we can't say that the rectangle has a 2d Euclidean area, can we say that it has a perimeter?

When you say Euclidean area, you are adding the 5 postulates of Euclidean geometry. Do you mean to do that? There are other geometries where perimeters are defined.

 

[Nugatory]

How does this not have to be a 2d Euclidean rectangle that I am describing?

With a Euclidean rectangle, if the sides have length $A$ and $B$, the lengths of the diagonals will be $\sqrt{A^2+B^2}$ - this is just the Pythagorean theorem at work.

But the Pythagorean theorem doesn't work with the Minkowski geometry; the diagonals of the rectangle will have length $\sqrt{|A^2-B^2|}$ which makes this rectangle very different from the 2d Euclidean rectangle.

 

[student34]

There are only two properties of the temporal dimension that distinguish it from the spatial dimensions:

1) there is only one temporal dimension
2) it has a different sign in the signature

Everything else stems from those two features.

Is 2) just a fact that time goes in a negative direction according to its coordinate system?

 

[PeterDonis]

Is 2) just a fact that time goes in a negative direction according to its coordinate system?

That's not what the different sign in the metric signature means. The different sign is on the squared timelike interval. It has nothing to do with "which direction time flows".

 

[student34]

You don't have to convince me that you don't need the extra spatial dimensions for the basic idea you are exploring. But you might need to convince yourself, since you said:Why should this trouble you if adding more dimensions just makes things needlessly more complicated?

I meant that 1d of space and 1d of time is challenging enough.

I've already told you: because Euclidean geometry is not the only possible geometry. The 2d "space" (or more precisely spacetime) that we are discussing here has Minkowskian geometry, not Euclidean geometry. That's just a physical fact. We know it's a physical fact because to properly model what happens in relativity, we need to use Minkowskian geometry; Euclidean geometry simply does not give the right answers.

Can we at least say that it is a rectangle? If we can, then can we say that this rectangle is on a plane?

So you think what a clock measures and what a ruler measures are the same thing? Why? Isn't it just obvious that these are physically different measurements of physically different things?

I meant length in terms of a length along a dimension. And why are they even physically different? A particle might be either a string through time or many identical particles next to each other (if spacetime is granular).

 

[PeterDonis]

Can we at least say that it is a rectangle?

As long as saying that does not imply that it is a Euclidean rectangle, sure.

If we can, then can we say that this rectangle is on a plane?

As long as saying that does not imply that the plane is a Euclidean plane, sure.

What's the point of all this?

I meant length in terms of a length along a dimension. And why are they even physically different?

I've already told you that. Please go back and read my previous posts again. If you honestly can't see how a clock and a ruler are physically different things measuring physically different quantities, this thread is pointless and we might as well close it.

A particle might be either a string through time or many identical particles next to each other (if spacetime is granular).

This is verging on personal speculation, which is off limits here.

Have you actually tried to study special relativity from a textbook?

 

[student34]

When you say Euclidean area, you are adding the 5 postulates of Euclidean geometry. Do you mean to do that? There are other geometries where perimeters are defined.

Well, to be honest, I am just going by what my brain is telling me is logical. Though I suppose that might be a thread all on its own.

 

[student34]

With a Euclidean rectangle, if the sides have length $A$ and $B$, the lengths of the diagonals will be #\sqrt{A^2+B^2}$- this is just the Pythagorean theorem at work. But the Pythagorean theorem doesn't work with the Minkowski geometry; the diagonals of the rectangle will have length$\sqrt{|A^2-B^2|}## which makes this rectangle very different from the 2d Euclidean rectangle.

Ok, that's interesting. I did not think of it that way. Just out of curiosity, from the point of view of the time dimension (if I can even say that), would A^2 be -A^2 and -B^2 be B^2? Or is the temporal distance intrinsically negative?

 

[robphy]

@student34 As others have suggested, now that your interest is piqued, it’s probably time to learn the physics behind the geometry…. From a proper textbook or other resource in relativity.

Once you understand the basic physics encoded by the geometry, you can then search for possible physical interpretations for other geometric features.
(My study of “area” was like this… and looking through the literature, I realized that aspects of this were known…
but not used in the way I have used it.)

Proceeding by pure logic without the guidance from the already established physics is likely to lead you through a random walk of possibilities… (where many of those possibilities have been ruled out by the established physics)… leading to little progress in understanding relativity.

My $0.02.

 

[FactChecker]

@student34 As others have suggested, now that your interest is piqued, it’s probably time to learn the physics behind the geometry…. From a proper textbook or other resource in relativity.

Once you understand the basic physics encoded by the geometry, you can then search for possible physical interpretations for other geometric features.
(My study of “area” was like this… and looking through the literature, I realized that aspects of this were known…
but not used in the way I have used it.)

Proceeding by pure logic without the guidance from the already established physics is likely to lead you through a random walk of possibilities… (where many of those possibilities have been ruled out by the established physics)… leading to little progress in understanding relativity.

My $0.02.

I like this advice, especially since the physical experiments led to conclusions and geometries that were not intuitive at the time.

 

[cianfa72]

We measure arc lengths along a timelike dimension using clocks.

Yes of course.

We measure arc lengths along a spacelike dimension using rulers. That is the physical difference between the two.

I believe the point to be highlighted is that the measurement of arc lengths along a spacelike dimension is not actually a "direct" measure. To do a such measurement we need a body/ruler that extend between the "endpoints" (i.e. the ruler's endpoints must coincide with the spacelike path endpoint events at the 'same time' as defined by the implied definition of simultaneity given by the spacelike path).

If we try to juxtapose rulers one after the other, what we do is connect events that cannot be spacelike separated (i.e. the process takes place along a timelike path).

 

[Sagittarius A-Star]

2) Is the rectangle a 2d Euclidean space?

Or is the temporal distance intrinsically negative?

No to both. A spacetime-diagram is a picture of physical reality. It is not exactly identical to it.

• The spatial (x,y)-coordinates on a paper belong to Euclidean geometry. The squared distance between two points on the paper is equal to $\Delta x^2 + \Delta y^2$.
• The spacetime (ct,x)-coordinates in reality have Minkowski-geometry (scenario without the other 2 spatial dimensions): The squared spacetime-interval between two events is either defined as $c^2\Delta t^2 - \Delta x^2$ or as $-c^2\Delta t^2 + \Delta x^2$. This is convention.

You must consider this difference between reality and a picture of it, when reading a spacetime diagram.

 

[Dale]

Is 2) just a fact that time goes in a negative direction according to its coordinate system?

It refers to the - sign in $ds^2=-dt^2+dx^2+dy^2+dz^2$. It also refers to the fact that time is measured with clocks while the three spatial dimensions are measured with rulers.

 

[vanhees71]

NO to item 1! For a Minkowski diagram the paper you draw it on is not "belonging to Euclidean geometry", because by definition the fundamental form put on top of the affine-manifold description is no longer positive definite but of the signature (1,1). That's what you say yourself in item 2, and it avoids a lot of confusion when you always keep in mind that at the moment when you use your paper to draw a Minkowski diagram it's no longer considered as described as an Euclidean but a Lorentzian 2D affine manifold.

 

[PeterDonis]

I am just going by what my brain is telling me is logical.

You can't trust what your brain is telling you is logical if your brain does not know about all of the logical possibilities. If your brain has never been taught anything about non-Euclidean geometries, your brain is going to wrongly tell you that the geometry of anything must be Euclidean. That's basically what's happening here.

If you want to understand relativity, you need to re-train your brain.

from the point of view of the time dimension (if I can even say that), would A^2 be -A^2 and -B^2 be B^2? Or is the temporal distance intrinsically negative?

The way you are asking this question is garbled, but I can rephrase it in better terms. When writing down the metric of Minkowski spacetime, there are two "signature conventions" you can adopt: the spacelike convention, in which spacelike squared intervals have a positive sign (and timelike squared intervals have a negative sign), or the timelike convention, in which timelike squared intervals have a positive sign (and spacelike squared intervals have a negative sign). Both are valid mathematical representations of the physics. Different references might prefer different conventions.

 

[student34]

As long as saying that does not imply that it is a Euclidean rectangle, sure.As long as saying that does not imply that the plane is a Euclidean plane, sure.

What's the point of all this?

In general, I want to understand what can be said about the space of the rectangle. I also want to know about the properties of the temporal dimension and the relationship between the temporal dimension and the spatial dimensions.

I've already told you that. Please go back and read my previous posts again. If you honestly can't see how a clock and a ruler are physically different things measuring physically different quantities, this thread is pointless and we might as well close it.

You said, "measurements of physically different things", I thought this meant what the device is measuring, not the device itself.

This is verging on personal speculation, which is off limits here.

That is not what I have read. I have read that this is an implication to relativity. What else would compose a particles' world line?

Have you actually tried to study special relativity from a textbook?

Yes, I took it in a first-year physics course at university.

 

[PeterDonis]

In general, I want to understand what can be said about the space of the rectangle. I also want to know about the properties of the temporal dimension and the relationship between the temporal dimension and the spatial dimensions.

In other words, you want to understand special relativity. That means that, as I said before, you should go learn it from a textbook. We can't give you a complete course in SR here; that's way beyond the scope of a PF thread.

You said, "measurements of physically different things", I thought this meant what the device is measuring, not the device itself.

It means both. You have physically different devices (clock and ruler) measuring physically different things (proper time vs. proper length).

That is not what I have read.

Read where? Please give a specific reference.

In SR, particles are represented as worldlines, which are timelike curves (or null curves if the "particles" are photons--light rays) in spacetime. Neither of the things you said are saying that ("string through time" could sort of be interpreted that way, but could also be interpreted other ways, and "spacetime is granular" is completely off topic for relativity, that's a speculation in quantum gravity for which there is no evidence).

 

[PeterDonis]

I took it in a first-year physics course at university.

Then I am flabbergasted that you would be asking the questions you are asking and would not understand the basics of Minkowskian geometry already.

 

[PeterDonis]

the measurement of arc lengths along a spacelike dimension is not actually a "direct" measure.

This is true, but you don't even need to get to this point to see that arc length along a spacelike curve is physically different from arc length along a timelike curve. Just the fact that you have two different measuring devices is enough. The points you raise are additional valid points that further emphasize the difference, yes.

 

[student34]

No to both. A spacetime-diagram is a picture of physical reality. It is not exactly identical to it.

• The spatial (x,y)-coordinates on a paper belong to Euclidean geometry. The squared distance between two points on the paper is equal to $\Delta x^2 + \Delta y^2$.
• The spacetime (ct,x)-coordinates in reality have Minkowski-geometry (scenario without the other 2 spatial dimensions): The squared spacetime-interval between two events is either defined as $c^2\Delta t^2 - \Delta x^2$ or as $-c^2\Delta t^2 + \Delta x^2$. This is convention.

You must consider this difference between reality and a picture of it, when reading a spacetime diagram.

Then this is where I am confused. It is said that we travel through time at c. In one second I "travelled" 299,792,458 meters through time. But then if I use the spacetime interval formula, I get an imaginary number. Ok, I think I can learn something new here.