How Do You Calculate Reactions at a Pin and Roller on an Inclined Beam?

[pleasehelpme6]

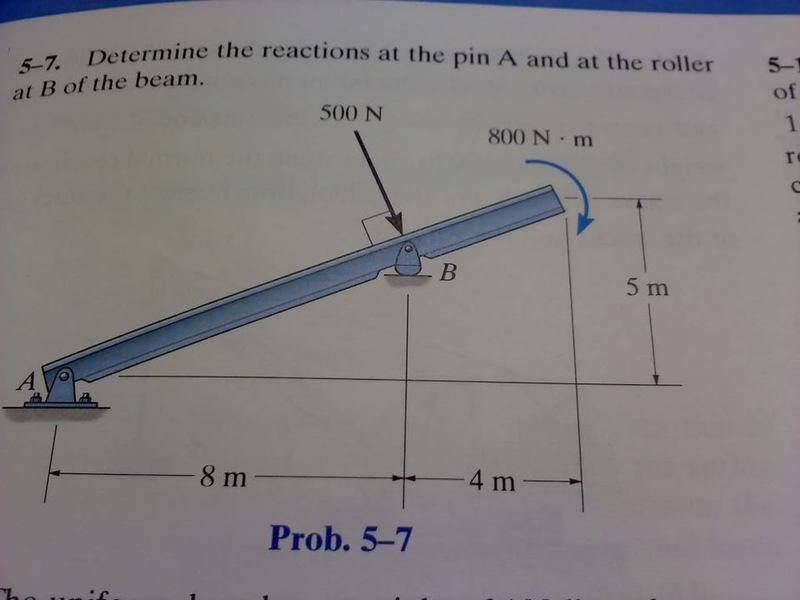
Determine the reactions at the pin A and at the roller at B of the beam.

I honestly have no idea how to do this problem.
It gives the answers as...

Ax = 192 N
Ay = 180 N
By = 642 N

Please help.

 

[PhanthomJay]

Heck, you've got to show something. Try listing the relevant equations. Note that the roller support can only provide vertical forces, not horizontal. The pin support can provide both. Use the equilibrium equations for forces and moments.

 

[adeolu2k5]

As phanthom jay said above you have a roller joint at point B so you have just a vertical reaction force Rby since it is a pin joint at point A you have reaction forces Ray and Rax. The beam is inclined at 22deg
The 500N force is resolved vertically giving 500/cos22

therefore
Rax=0
SUM horizontal forces
Ray + Rby=500/cos22

SUM moment of forces about Point B
Ray.8 - Rax.3.33=800

so i get
Rax=0N
Rbx=0N
Ray=-100N
Rby= 1434.7N