Reflection factor for a microstrip transmission line

[Amalogon]

I have a problem here where I would like to calculate the reflection coefficient (marked as r in the image below). This should equal according to a formula from which I am unsure if it is true:

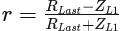
where ZL1 is the first microstrips wave impedance and RLast should be (if I didn't misunderstood the formula) the load on the other side of the first microstrip conduction line.
So much for the theory. Now, in my opinion, R_Last should be half of the series circuit of the microstrips wave impedances ZL2 and ZL3 and the terminating resistor Rv

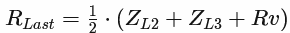
However, according to a solution I have, this does not seem to be the case. According to this solution, RLast should be only half of ZL2. Why? Is this even the case?

Here is my sketch of the circuit in microstrip technology (L2 and L3 should simply mark the lengths of the respective conductors here; all conductors are assumed to be lossless):

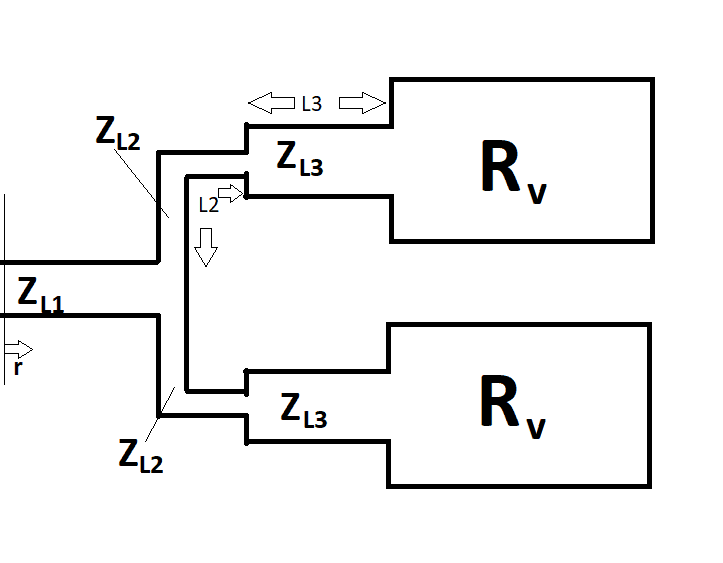
The deeper sense of the task is to calculate ZL2 as a function of ZL1 if wave matching is to exist ( thus r is zero at all times), independent of the length L2.

 

[Baluncore]

Welcome to PF.

My guess is that the generator has an impedance of Rlast, and is off the diagram to the left, driving the input line ZL1. That equation is then the reflection coefficient, from ZL1 back to the generator.

ZL1 ends in a power divider, with two lines, each of ZL2.
Maybe ZL2 = 2 * ZL1.

I would expect ZL3 to be a quarter-wave-transformer, matched to Rv/2 . With impedance ZL3 = √2 * ZL2.

It looks a bit like a Wilkinson divider, but there are no output ports.
https://en.wikipedia.org/wiki/Wilkinson_power_divider

So I do not know where the divided energy goes from there, or how many Rv terminations there are, to what.

Maybe you misunderstood the question.
Where does the original question come from? Link?
Is this homework?

 

[Amalogon]

First, thank you for the answer.

Well yes, this is kind of homwork (more precise part of an exercice from an old exam). Thus I cannot really share a link to it.

[Mentor Note: Thread moved to the schoolwork forums now]

Talking about the exercice: Is it in fact relevant what impedance we have in front (on the left side) of the microstrip conductors? Since here, the reflection factor r should be equal to zero (according to the exercice), there is no power reflected back to the generator, why I assume that it's impedance shouldn't here really matter.

What interest us here, is the meaning of the different impedances from the equation of the reflection factor, as it can also be seen here on the wikipedia: https://en.wikipedia.org/wiki/Reflection_coefficient (under section: relation to load impedance). While I can understand what Z0 should be (in my example it is called ZL1), I cannot understand what the ZL (in my case it is called ZLast) is.

If I could understand what the Z0 and ZL is, think I would be able to solve the exercice on my own.

 

[Tom.G]

...If I could understand what the Z0 and ZL

That Z₀ (Z _zero) generally indicates the impedance of what you are trying to match (the source impedance), and the Z_L is the impedance of the Load on what you are trying to match.

The deeper sense of the task is to calculate ZL2 as a function of ZL1 if wave matching is to exist ( thus r is zero at all times), independent of the length L2.

Think parallel and series resistors here. Being RF, an added requirement is that Rv, Z_L3, and Z_L2 need to be matched to each other to avoid reflections at their junctions.

https://en.wikipedia.org/wiki/Reflection_coefficient

above found with:
https://www.google.com/search?hl=en&source=hp&biw=&bih=&q=microwave+reflection+coefficient

Hope this helps!

Cheers,
Tom

 

[Amalogon]

That Z0 (Z zero) generally indicates the impedance of what you are trying to match (the source impedance), and the ZL is the impedance of the Load on what you are trying to match.

Okay. In other words, Z0 is in this case ZL1 because we are trying to match it. I think that's clear.
You have written that ZL is the impedance of the load on what we are trying to match. Well, I think it is still unclear for me, why solely ZL2 is that load, and not ALSO the serial resistors behind? I want to point out that here, the lengths L2 (the length of the second microstrip with ZL2) shouldn't have any influence on ZL4, according to the exercices task. Could this be the reason why the serial restistors behind ZL2 doesn't matter as load? I'm having serious trouble understanding this.

 

[Joshy]

independent of the length L2.

This part is super important for your question. Lets take a step back and look at a transmission line I'll call ZL2, which has a characteristic impedance Z2, an arbitrary length L, and its load is ZL. What are some things I can do to make its impedance stay the same for different values of L? I'm ignoring everything else in your problem just for a second to try and understand this one part so that the problem becomes easier to digest.

Let me give you an example. Lets say ZL2 is 100 Ohm transmission line and I load it with 50 Ohms. If I made L = quarter-wavelength, then the impedance would look like 200 Ohms. If I made L = half-wavelength, then it would look like 50 Ohms. If I made L = (1/3) wavelength, then the impedance would be this totally wild 114.286 - j74.231. So you can see here that my transmission line it is dependent on the length of ZL2. What would I need to do to fix that so length doesn't matter?

By the way: Transmission lines are NOT lumped element circuits. When I say lumped element circuits I am meaning like the ones in your very introductory circuit classes with a few resistors in series that you can add together... so the impedance in your transmission line problem is not going to look like Z2 + Z3 + Rv outside of a very special condition. It's distributed element (it's composed of many little R', L', G', and C' these are per unit length). Noticed how when I changed the length of the transmission line in my example I could make a 50 Ohm resistor look like 114.286 - j74.231. This is usually the eye-opening point in the class(es) that cover this topic, and it's very important to understand this.

Did the professor or the book you are following cover the equation to solve for the impedance of a loaded transmission line? It usually looks something like this Zin = Z0 * (ZL + jZ0 tan( ... sometimes if it's not covered yet or professor wants to keep it simple, then they might cover a few special cases like the quarter-wave QW circuit Baluncore mentioned, and being aware of a few special cases would be good enough for a problem like this.

 

[Amalogon]

Did the professor or the book you are following cover the equation to solve for the impedance of a loaded transmission line? It usually looks something like this Zin = Z0 * (ZL + jZ0 tan( ...

Yes, we did. If we have a transmission line like this one...

... then (assuming that the transmission line is lossless) we get for Zinside:

However, also with this equation, I still have the problem to understand, why Zload is only 1/2*ZL2 and not 1/2*(ZL2+ZL3+Rv)

What would I need to do to fix that so length doesn't matter?

If Zload = ZL, then Zinside equals Zload and thus is independent from L.

 

[Joshy]

You're in the home-stretch. Almost there!

Your notation for this stuff is very strange by the way, but I can see in the equation you discriminate between ZL and Zload. Most people don't do the notation that way. They'll probably prefer the way that I have it above. They usually use Z0 in place of where you are using ZL in your equation in #7. If you use ZL and Zload as two different things that is very confusing because most people literally consider ZL and Zload the same thing. So lets shift that over to my notation so we don't confuse other readers. In your last post #7 everything you are calling ZL lets replace that with Z0. Each transmission line or different stages might have its own Z0, and so I am call it Z0,N where N is the stage number. If we want to be lazy we can call it ZN where N is also the stage number.

So you got it right: the load impedance must match the characteristic impedance (ZL = Z0), and just to clarify this is per stage. So if you want it to be length independent at stage 2, then you must make the load right at the end of stage 2 equal to its characteristic impedance Z0,2. So whatever is going on with stage 3 and Rv when they tell you that stage 2 has no length dependence, then all that stuff over there you know it's going to have to equal something to fulfill that length indepence requirement.

Since the load impedance is Z0,2 and the length doesn't matter anymore you can travel it all the way down to the end of stage 1 (which is where I think you are calling its Zin as Rlast), and you have 2 parallel circuits with a certain load impedance (try it out in your equation make Z0 = ZL and you will see that you can do this!) I think you can connect the dots from there.

Remember: The eye-opener to the classes that cover this topic is that you cannot just treat this like the simple lumped element circuits; so: It's a ginormous mistake to be asking why you can't add the characteristic impedance in series. It doesn't work like that at all. Don't confuse characteristic impedance with (regular) impedance. It's not the same thing even though the names are similar