- #1
peripatein
- 880
- 0
Hi,
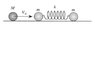
I'd like to find the minimum mass M which will render possible a second collision between M and the two masses m and the spring in the attachment, and also the time between the two collisions. It is stated that the initial velocity of M is v0 as indicated and that the surface is frictionless. It is also stated that this is an elastic collision, whose time is very short. M doesn't get attached to the masses.
I am not quite sure how to formulate a condition on M, which will enable a second collision. I am not even sure how a second collision would be possible unless there were let's say a wall on the other side hitting M back towards the masses and the spring. The kinetic energy of M is turned into an elastic energy of the spring and kinetic energy of both M and the reduced mass = m/2, right (due to conservation of energy)?
Furthermore, there is conservation of linear momentum, isn't there?
Must I work in the CM reference frame?
Homework Statement
I'd like to find the minimum mass M which will render possible a second collision between M and the two masses m and the spring in the attachment, and also the time between the two collisions. It is stated that the initial velocity of M is v0 as indicated and that the surface is frictionless. It is also stated that this is an elastic collision, whose time is very short. M doesn't get attached to the masses.
Homework Equations
The Attempt at a Solution
I am not quite sure how to formulate a condition on M, which will enable a second collision. I am not even sure how a second collision would be possible unless there were let's say a wall on the other side hitting M back towards the masses and the spring. The kinetic energy of M is turned into an elastic energy of the spring and kinetic energy of both M and the reduced mass = m/2, right (due to conservation of energy)?
Furthermore, there is conservation of linear momentum, isn't there?
Must I work in the CM reference frame?