Request about experiments on the linear-motion Faraday paradox

[greswd]

The Faraday paradox is a very curious example in the topic of relative motion.

An experiment demonstrating the curious results is shown in the video below:
This has made me curious about the linear version of the Faraday paradox.
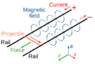
A conductor placed atop a magnet, both at rest in one scenario. In another, both moving together in uniform linear motion.

The linear scenario is expected to produce very different results from the rotational scenario.

Therefore, I'm also interested in the transition from linear to rotational motion and vice versa.
Small segments of a circular arc approximate straight lines, small segments of rotational motion approximate linear motion.

Experiments of the transitional scenarios should ostensibly yield explanations as to why the two scenarios produce different results.

Thus, so far, what results have such experiments yielded?

 

[BvU]

Not clear to me if you watched part 2 as well ?

 

[greswd]

Not clear to me if you watched part 2 as well ?

I have, it doesn't mention any linear or transition experiments afaia.

 

[BvU]

My bad, I focused on the video. Linear motion is even easier (I assume you don't intend to go to relativistic speeds and Lorentz transforms).
Same Lorentz force expression.

Check this thread

 

[olgerm]

linear version of the Faraday paradox.
A conductor placed atop a magnet, both at rest in one scenario. In another, both moving together in uniform linear motion.

Where is the voltage measured? aka where would wires to voltmeter be connected?

You should consider, that $\vec{\epsilon}=\frac{E}{q}=\int(dl \frac{F}{q})=\frac{\int(dl (E+v\times B))}{q}$ and maxwell equations.

In 1. case E=0 and v=0. So $\epsilon$ must be 0.

 

[greswd]

My bad, I focused on the video. Linear motion is even easier (I assume you don't intend to go to relativistic speeds and Lorentz transforms).
Same Lorentz force expression.

Check this thread

No worries. In rotational motion, the conductor and magnet moving together generates EMF. In linear motion, I guess it is zero EMF.
I'm curious about the experimental results in transitional cases.

 

[greswd]

Where is the voltage measured? aka where would wires to voltmeter be connected?

You should consider, that $\vec{\epsilon}=\frac{E}{q}=\int(dl \frac{F}{q})=\frac{\int(dl (E+v\times B))}{q}$ and maxwell equations.

In 1. case E=0 and v=0. So $\epsilon$ must be 0.

Could be one wire at each end of the conductor plate, and the setup being moved perpendicular to the connective line.

That means a velocity vector perpendicular to an imaginary line connecting both wires across the plate.

I don't know if the wire ends being connected to the moving plate or scraping along the surface of the moving plate makes a difference.

 

[BvU]

in transitional cases

transitional results.

 

[greswd]

transitional results.

Lol. But in all seriousness, someone ought to have investigated this before.

 

[olgerm]

$\vec{\epsilon}=\frac{E}{q}=\int(dl \frac{F}{q})=\frac{\int(dl (E+v\times B))}{q}$ and maxwell equations.

it should be that
$\epsilon=\frac{E}{q}=\oint(dl \frac{F}{q})=\oint(dl (\vec{E}+\vec{v}\times \vec{B}))$

 

[greswd]

it should be that
$\epsilon=\frac{E}{q}=\oint(dl \frac{F}{q})=\oint(dl (\vec{E}+\vec{v}\times \vec{B}))$

ah ok, thanks
by the way, how do you think the transition occurs?

 

[olgerm]

ah ok, thanks
by the way, how do you think the transition occurs?

What do you mean by transition?

 

[olgerm]

To measure voltage or generate eletricity you need a closed circut.
$U=\oint(dl*(\vec{E}+\vec{v}\times \vec{B}))=\oint(dl*\vec{E})+\oint(dl*(\vec{v}\times \vec{B}))=\frac{\partial \oint (dS*\vec{B})}{\partial t*c}+\oint(dl*(\vec{v}\times \vec{B}))$. I do not see how yet, but I think that if you simplify it more you may get that U=0. U is voltage.

 

[greswd]

What do you mean by transition?

The linear case is expected to give different results from the rotational case. But I wonder about the transition, in between those two cases.

 

[jartsa]

If we zoom into a small area on an average sized Faraday disk, we will see just some co-moving particles, so we can say that it's not the magnet straight below the conductor that causes a Lorentz-force on the charges.

So we can guess it's the other parts of the magnet. Those parts of the magnet that are in motion relative to the part of the conductor that we are zooming into.

 

[olgerm]

To measure voltage or generate eletricity you need a closed circut.
$U=\oint(dl*(\vec{E}+\vec{v}\times \vec{B}))=\oint(dl*\vec{E})+\oint(dl*(\vec{v}\times \vec{B}))=\frac{\partial \oint (dS*\vec{B})}{\partial t*c}+\oint(dl*(\vec{v}\times \vec{B}))$. I do not see how yet, but I think that if you simplify it more you may get that U=0. U is voltage.

Should be that:
$U=\oint(dl*(\vec{E}+\vec{v}\times \vec{B}))=\oint(dl*\vec{E})+\oint(dl*(\vec{v}\times \vec{B}))=\oint(dl*(\vec{v}\times \vec{B}))-\frac{\partial \oint (dS*\vec{B})}{\partial t}$

U is not 0 in all closed circuts only if $rot(\vec{v}\times \vec{B})-\frac{\partial \vec{B}}{\partial t}=\vec{v}(\nabla \cdot \vec{B}) - \vec{B}(\nabla \cdot \vec{v}) + (\vec{B}\cdot \nabla)\vec{v} - (\vec{v}\cdot \nabla)\vec{B}-\frac{\partial \vec{B}}{\partial t}$

according to Maxwells II equation div(B)=0 the expression simplifies to:
$rot(\vec{v}\times \vec{B})-\frac{\partial \vec{B}}{\partial t}=\vec{B}(\nabla \cdot \vec{v}) + (\vec{B}\cdot \nabla)\vec{v} - (\vec{v}\cdot \nabla)\vec{B}-\frac{\partial \vec{B}}{\partial t}$

since the idea based on a rigid body $div(\vec{v})=0$ the expression simplifies to:
$rot(\vec{v}\times \vec{B})-\frac{\partial \vec{B}}{\partial t}=\vec{B}(\nabla \cdot \vec{v})+(\vec{v}\cdot \nabla)\vec{B}-\frac{\partial \vec{B}}{\partial t}$

Since we assume that all EM field is created by the magnet and magnetic field is soly determined by position of magnet, $B(t)=f(\vec{X_{magnet}}(t))$ time $\Delta t$ ago was $B(t-\Delta t)=f(\vec{X_{magnet}}(t-\Delta t))=f(\vec{X_{magnet}}(t)-\Delta t*v)$, it must be that $(\vec{v}\cdot \nabla)\vec{B}=\frac{\partial \vec{B}}{\partial t}$ the expression simplifies to:
$rot(\vec{v}\times \vec{B})-\frac{\partial \vec{B}}{\partial t}=\vec{B}(\nabla \cdot \vec{v})=\vec{B}\cdot \omega$

if the body is moving lineary(not spinning) $\omega=0$ the expression simplifies to:
$rot(\vec{v}\times \vec{B})-\frac{\partial \vec{B}}{\partial t}=0$

Therefore the linear generator does not work. Maxwell equations+ and loretz force confirm that in both frames of reference.

 

[olgerm]

I'm curious about the experimental results in transitional cases.

The linear case is expected to give different results from the rotational case. But I wonder about the transition, in between those two cases.

Only the angular speed is important, whether the body is moving lineary at same time is not important.

 

[jartsa]

Only the angular speed is important, whether the body is moving lineary at same time is not important.

If we were to reverse a film about a fast spinning Faraday disk breaking into pieces, then we would have a film about many small linear Faraday generators becoming one large Faraday generator.

At the beginning of this film the generators would not produce anything (no Lorentz-force is produced). At the end of the film the generator works like a Faraday generator is supposed to work (there is a Lorentz-force).

So between the beginning and the end there must be a transition occurring. The system is in an interesting transitional state.

 

[artis]

The video is a bit misleading I think because keeping the magnet and disc stationary while simply moving the brushes should not generate current due to lorentz force , at least not from the disc as the electrons in the disc don't experience any force in such a situation , so I think he is picking up "noise" from the wires wiggling in a surrounding B field.

Also I have understood that the Faraday disc is very interesting with regards that it involves special relativity because there is only EMF and current when the disc is closed with a return path that rotates with a different speed or is stationary with respect to the disc , in other words there always must be relative motion between the two sides. In fact I think you can have a linear homopolar generator/Faraday disc but you must provide electrical contacts to the metal sheet sliding atop a stationary or moving magnet and the contacts and the wire connecting them must be stationary or move with a different speed than the sheet.

Look at this simple "railgun" which is basically a linear homopolar motor/Faraday disc, if one applies current to the rails the third shunting rod moves along the rails, but if one puts a voltmeter across the rails, puts a magnet under or above the rails and moves the third rod by hand the voltmeter should read DC voltage output because imagine the rails , voltmeter and moving rod form a rectangular loop that is electrically closed , as you move the rod you change the cross-sectional area of the loop in other words you change the amount of B field lines through the loop which results in generated current in the loop.
I think this is what happens..
Also as the OP said , a large enough disc resembles a linear metal wire or sheet moving in a B field if small portions/slices are considered of the disc and again they too would need a closing loop rotating at different speed to have any current in the loop or force exerted by the slice to move.

 

[jartsa]

The video is a bit misleading I think because keeping the magnet and disc stationary while simply moving the brushes should not generate current due to lorentz force , at least not from the disc as the electrons in the disc don't experience any force in such a situation , so I think he is picking up "noise" from the wires wiggling in a surrounding B field.

Return path moves relative to a magnet, so voltage is generated in the return path. Disk does not move relative to a magnet, so there is no voltage generated, so there is no voltage that could cancel that one voltage, so there is a voltage in the circuit.
I have a question: Does a spinning disk shaped magnet generate a Lorentz-force on a metal rod above it?

Or do the many microscopic Lorentz-forces that the many microscopic magnets inside the disk-magnet exert on the charges inside the rod cancel out each other?

If they cancel out, then I made an error earlier in post #13.

 

[artis]

Personally I don't think any force is exerted on the rod above the magnet apart from if it is from a ferromagnetic material is will feel attraction to the magnet.
My theoretical knowledge is not perfect so I can't say but from what I have read from experiments, spinning a magnet around it's axis doesn't change the field , if the magnet is symmetrical then the field is homogeneous and symmetrical and physically rotating the magnet material doesn't change that. Treat the rod above the magnet as part of a disc so there is no difference and as far as we know if the disc does not spin itself then there is no current generated. To the best of my knowledge.

In other words the B field is static because it's strength doesn't change , it is symmetrical and homogeneous, for the electrons in a stationary conductor to feel a force they need to either move themselves through a B field or have a B field that changes strength or polarity with time so a time varying field , but here we have a stationary field and a stationary conductor.

 

[olgerm]

If we were to reverse a film about a fast spinning Faraday disk breaking into pieces, then we would have a film about many small linear Faraday generators becoming one large Faraday generator.
At the beginning of this film the generators would not produce anything (no Lorentz-force is produced). At the end of the film the generator works like a Faraday generator is supposed to work (there is a Lorentz-force).
So between the beginning and the end there must be a transition occurring. The system is in an interesting transitional state.

the generator is producing electricity if charge-carrying material(disc) between stator(brush) and center of disc is moving crosswise to vector from stator(brush) to center of the disc.
If disc break into pieces and there is non-conductive material between pieces the generator does not produce electricity because there is no connection between stator(brush) and center of the disc.

 

[greswd]

the generator is producing electricity if charge-carrying material(disc) between stator(brush) and center of disc is moving crosswise to vector from stator(brush) to center of the disc.
If disc break into pieces and there is non-conductive material between pieces the generator does not produce electricity because there is no connection between stator(brush) and center of the disc.

but there could be an EMF within a broken piece, causing the piece to become polarized.

 

[greswd]

If we were to reverse a film about a fast spinning Faraday disk breaking into pieces, then we would have a film about many small linear Faraday generators becoming one large Faraday generator.

At the beginning of this film the generators would not produce anything (no Lorentz-force is produced). At the end of the film the generator works like a Faraday generator is supposed to work (there is a Lorentz-force).

So between the beginning and the end there must be a transition occurring. The system is in an interesting transitional state.

yes! you got it!

 

[greswd]

I have a question: Does a spinning disk shaped magnet generate a Lorentz-force on a metal rod above it?

According to the video, spinning the magnet does nothing. @artis

 

[greswd]

if the body is moving lineary(not spinning) $\omega=0$ the expression simplifies to:
$rot(\vec{v}\times \vec{B})-\frac{\partial \vec{B}}{\partial t}=0$

Therefore the linear generator does not work. Maxwell equations+ and loretz force confirm that in both frames of reference.

Sorry, why does this mean that the linear generator does not work?

To me it seems to only state that $rot(\vec{v}\times \vec{B})=\frac{\partial \vec{B}}{\partial t}$

 

[olgerm]

Sorry, why does this mean that the linear generator does not work?
To me it seems to only state that $rot(\vec{v}\times \vec{B})=\frac{\partial \vec{B}}{\partial t}$

because to produce electricity you need a closed circuit in which electromotive force(U) is not 0. U can be expressed as $U=\oint(dl*(\vec{E}+\vec{v}\times \vec{B}))=\oint(dl*\vec{E})+\oint(dl*(\vec{v}\times \vec{B}))=\oint(dl*(\vec{v}\times \vec{B}))-\frac{\partial \oint (dS*\vec{B})}{\partial t}$.
If you take smaller circuits and connect these together then EMF of the new circuit is sum of the smaller circuits. EMF infinitesimaly small circuit is $rot(\vec{v}\times \vec{B})-\frac{\partial \vec{B}}{\partial t}$ and I showed that all these have 0 EMF. All closed circuits can be composed of infinitesimaly small circuits. Therefore all closed circuits must have 0 EMF.

 

[greswd]

because to produce electricity you need a closed circuit in which electromotive force(U) is not 0. U can be expressed as $U=\oint(dl*(\vec{E}+\vec{v}\times \vec{B}))=\oint(dl*\vec{E})+\oint(dl*(\vec{v}\times \vec{B}))=\oint(dl*(\vec{v}\times \vec{B}))-\frac{\partial \oint (dS*\vec{B})}{\partial t}$.
If you take smaller circuits and connect these together then EMF of the new circuit is sum of the smaller circuits. EMF infinitesimaly small circuit is $rot(\vec{v}\times \vec{B})-\frac{\partial \vec{B}}{\partial t}=\vec{v}(\nabla \cdot \vec{B}) - \vec{B}(\nabla \cdot \vec{v}) + (\vec{B}\cdot \nabla)\vec{v} - (\vec{v}\cdot \nabla)\vec{B}-\frac{\partial \vec{B}}{\partial t}$ and I showed that all these have 0 EMF. All closed circuits can be composed of infinitesimaly small circuits. Therefore all closed circuits must have 0 EMF.

I refer to my earlier post:

but there could be an EMF within a broken piece, causing the piece to become polarized.

All the linear-motion pieces could be expected to be polarized.

 

[olgerm]

All the linear-motion pieces could be expected to be polarized.

This was about linear motion scenario not about disc breaking scenario.

 

[artis]

I believe the linear moving sheet also becomes polarized just like the disc becomes, in both cases any current can be measured or generated only when the circuit is closed with a conducting path that is either stationary with respect to the moving part of the circuit or moving with a different speed, the generated voltage will then be equal to the field strength and the difference in speed between the two parts of the circuit, the larger the difference in speed the higher the voltage.The reason I say that the Faraday generator can be also made linear is because there exists a Faraday disc/homopolar generator whose geometry is so called "drum" type instead of axial disc type. Basically a conductive tube or cylinder is rotating around it's vertical axis, the field must then be either from inside out or outside in and the cylinder cuts the field at 90 degrees just like the disc does , again we get generated current if brushes are applied at both ends of the cylinder. Theoretically one can imagine this cylinder being cut open along it's axis and rolled out flat becoming a sheet of metal and the same current generating principles would apply, as long as there are brushes and two parts of a circuit that move with different speed.

 

[greswd]

I believe the linear moving sheet also becomes polarized just like the disc becomes

the problem is, that might be a violation of the principle of relativity

 

[greswd]

This was about linear motion scenario not about disc breaking scenario.

Well, we ought to investigate the transition cases.

 

[olgerm]

Well, we ought to investigate the transition cases.

Depends what will be between the pieces, what is capacity of pieces, what shape the pieces are and etc.

 

[greswd]

Depends what will be between the pieces, what is capacity of pieces, what shape the pieces are and etc.

yeah, you can set your own parameters.

The issue is how to not violate the principle of relativity.

 

[olgerm]

yeah, you can set your own parameters.The issue is how to not violate the principle of relativity.

How could it violate principle of relativity? Set your own parameters and explain how it does violate principle of relativity.