umzung
- 21
- 0
- Homework Statement
- How does one bracket become the other?
- Relevant Equations
- See the attempt at a solution.
How does
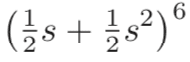 become
become
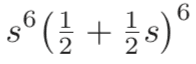 ?
?
I can see the s has been factored out and the power of 6 distributed, but how do we know this happens, short of multiplying out the brackets?
I can see the s has been factored out and the power of 6 distributed, but how do we know this happens, short of multiplying out the brackets?