Rotation of a Solid Cylinder

[brotherbobby]

Problem :

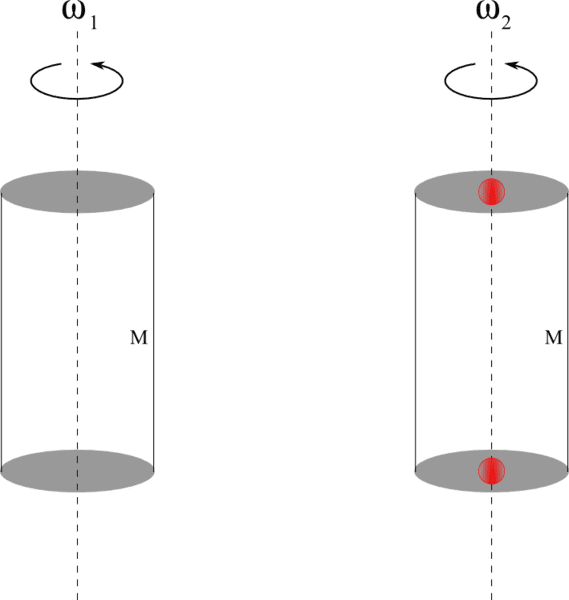
A cylinder of mass $M$ and radius $R$ rotates with an angular velocity $\omega_1$ about an axis passing through its centre of symmetry. Two small masses each of mass $m$ (small in comparison to the radius of the cylinder) are glued to either of the two circular faces of the cylinder right on its axis of rotation. The cylinder-mass system now rotates with an angular velocity $\omega_2$.
Is $\omega_2$ greater than, less than or equal to $\omega_1$?

Relevant equations :

The moment of inertia of the solid cyliner is $\frac{1}{2} MR^2$. My attempt :

The two small masses do not increase the moment of inertia of the cylinder, being point masses. Hence $\omega_2$ = $\omega_1$

 

[Orodruin]

Your problem is ill defined. What else is given in the problem? Obviously you can rotate either setup with whatever angular velocity you want, it just depends on how much angular momentum you put into the system. You need to specify what other assumptions should be taken, such as same angular momentum.

 

[BvU]

The exercise is incomplete: they don't tell you what remains constant. However small, the extra masses definitely do not decrease the moment of inertia and do contribute to it. There is a good argument to claim $\omega_2 < \omega_1$.

 

[brotherbobby]

Will the moment of inertia of the combined system be more than that of the bare cylinder?

 

[BvU]

Check the definition

 

[brotherbobby]

If the two masses lie along the axis of the cylinder, then they won't contribute to the moment of inertia (about that axis).

 

[BvU]

 

[brotherbobby]

Yes, but these are point masses. They have no radius of their own. They are put along the axis of the cylinder.

 

[BvU]

point masses don't exist and a small mass is not a point mass

 

[Orodruin]

Yes, but these are point masses. They have no radius of their own. They are put along the axis of the cylinder.

Correct. They have a radius, but it is considered negligible compared to that of the cylinder.

small in comparison to the radius of the cylinder

In this case, negligible means that $MR^2 \gg mr^2$, so it is actually an issue of both mass and radius ...

 

[brotherbobby]

True, if you insist that the masses have a radius, they will contribute to I. But the question is about point masses.

 

[BvU]

Then you won't need much glue

 

[Orodruin]

It would be fair to call this entire argumentation ...(drumrolls please)... pointless ...

Anyway, I think it is clear from the formulation of the problem that the additional masses should be considered to give a negligible contribution to the moment of inertia. What is missing, as already stated, is the assumption about what is supposed to be considered constant.