hquang001
- 31
- 3
- Homework Statement
- Two 2.00 kg balls are attached to the ends of a thin rod of length 50.0 cm and negligible mass. The rod is free to rotate in a vertical plane without friction about a horizontal axis through its center. With the rod initially horizontal, a 50.0 g wad of wet putty drops onto one of the balls, hitting it with a speed of 3.00 m/s and then sticking to it.
(a) What is the angular speed of the system just after the putty wad hits?
(b) What is the ratio of the kinetic energy of the system after the collision to that of the putty wad just before?
( c) Through what angle will the system rotate before it momentarily stops?
- Relevant Equations
- [tex] L_{initial} = L_{final} [/tex]
[tex] K_{initial} + PE_{initial} = K_{final} + PE_{final} [/tex]
mball = 2 kg, mputty = 0.05 kg, L = 0.5 m, v = 3m/s
a) Moment of inertia : I = (2mball + mputty ). ¼ L^2 = 0.253125 kg.m^2
Linitial = Lfinal => mputty. v. r = I.ω => ω = (4.mputty.v.r) / I = 0.148 rad/s
b) K initial = 1/2 m v^2 = 0.225 J
K final = 1/2 Iω^2 = 2.85.10^(-3) J => Kfinal / Kinitial = 0.013
c) Using conservation of energy :K initial +PE initial = K final + PE final
1/2 I.ω^2 + 0 = 0 + (mball + mputty).g.(-h) + mball.g.h
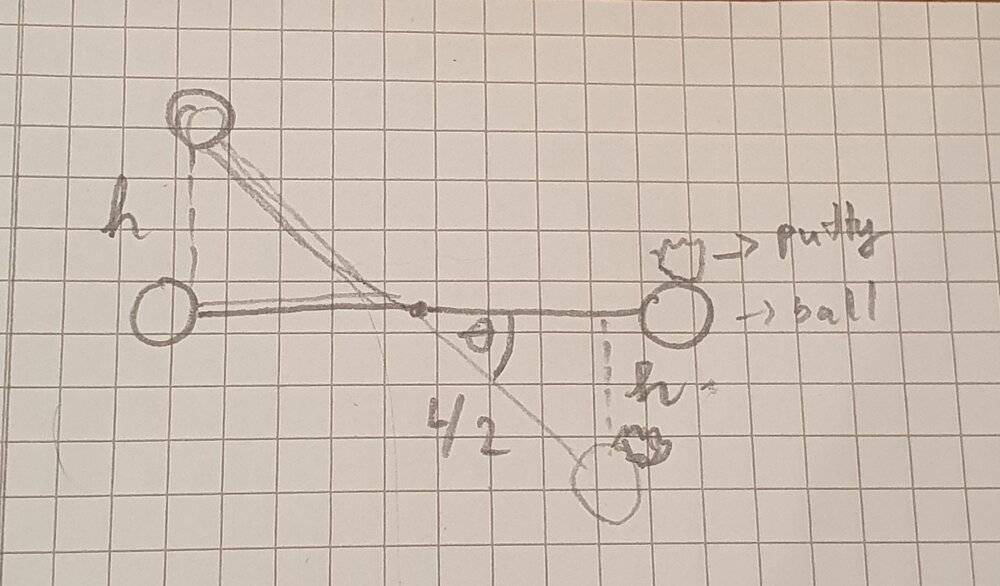
1/2 I.ω^2 = (2.05).g. (-sinΘ . L/2 ) + (2).g.(sinΘ . L/2)
=> 1/2 I.ω^2 = g.sinΘ . L/2 . (2 - 2.05) => Θ = -1.3°
I think the angle should be larger than 180 => 180° - (-1.3°) = 181°
I don't know if my answer for question c is correct or not
a) Moment of inertia : I = (2mball + mputty ). ¼ L^2 = 0.253125 kg.m^2
Linitial = Lfinal => mputty. v. r = I.ω => ω = (4.mputty.v.r) / I = 0.148 rad/s
b) K initial = 1/2 m v^2 = 0.225 J
K final = 1/2 Iω^2 = 2.85.10^(-3) J => Kfinal / Kinitial = 0.013
c) Using conservation of energy :K initial +PE initial = K final + PE final
1/2 I.ω^2 + 0 = 0 + (mball + mputty).g.(-h) + mball.g.h
1/2 I.ω^2 = (2.05).g. (-sinΘ . L/2 ) + (2).g.(sinΘ . L/2)
=> 1/2 I.ω^2 = g.sinΘ . L/2 . (2 - 2.05) => Θ = -1.3°
I think the angle should be larger than 180 => 180° - (-1.3°) = 181°
I don't know if my answer for question c is correct or not
Last edited: