Second order correction to the wavefunction

[robbo96]

Hi all,

I've been doing a lot of thinking and I was wondering precisely how the 2nd order correction to the wave function from perturbation theory is derived:

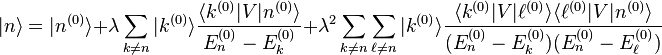
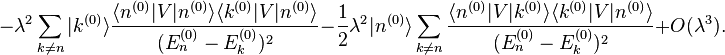
I mean, I can see where bits and pieces come from and I've tried to work through it as an exercise. Does anyone have a reference text on this that they can point me in the direction of? I've exhausted myself looking.

thanks!


Robert

 

[Avodyne]

http://www.physics.thetangentbundle.net/wiki/Quantum_mechanics/time-independent_perturbation_theory

Note that this calculation uses the normalization $\langle n|n^{(0)}\rangle=1$, and the result is missing your last term. This comes from changing the normalization to $\langle n|n\rangle=1$.