2013
- 92
- 0
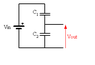
Qc = Q1 - Q2 = 2.915 x 10-10 C - 2.915 x 10-10 C = 0
Cc = Qc/Vc = 0/0,15V = 0
I don´t think that this is right. I do not think that the extra capacity is not zero, right?
Cc = Qc/Vc = 0/0,15V = 0
I don´t think that this is right. I do not think that the extra capacity is not zero, right?