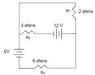
- #1
Ryoblck
- 29
- 0
Homework Statement
A. Make a prediction about the direction of current flow through each resistor. (6 points)
B. What current flows through each resistor? (15 points)
C. What is the voltage drop across R2? (4 points)
Homework Equations
Req=R1+R2+R3
The Attempt at a Solution
I'm sort of lost as to how to go about the equation. Normally I could tell the direction of the current when given a positive or negative sign near the battery.