Shell Method Example: Finding Volume Around Axes and a Line

[stripedcat]

I don't need the answers or the problems worked out I'm asking something more basic. This is just an example problem.

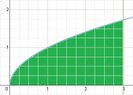
[math]y=\sqrt(x),y=0, x=3[/math]

a) Around the x-axis

[math]R(x)=\sqrt{x}, r(x)=0[/math]

I understand the R to be the value fathers from the x-axis, and the r value to be the closer one to the x-axis.

b) Around the y-axis

$$R(y)=3$$

This is because the right hand side of the bound region resists at x=3, which is the furthest away.

[math]r(y)=y^2[/math]

This is what I'm not clear on. How as this determined?

c) Around the line x=3

R(y)3-y^2

Not sure on that one either?

 

[MarkFL]

I would first begin by graphing the area to be revolved:

View attachment 2605

Now, if we are going to revolve about the $x$-axis, we may choose the disk method, where the volume of an arbitrary disk is:

$$dV=\pi r^2\,dx$$

where:

$$r=y=\sqrt{x}$$

hence:

$$dV=\pi x\,dx$$

Adding up all the disks, we get the volume:

$$V=\pi\int_0^3 x\,dx=\frac{\pi}{2}\left[x^2\right]_0^3=\frac{9\pi}{2}$$

Now, we could have chosen to use the shell method, where the volume of an arbitrary shell is:

$$dV=2\pi rh\,dy$$

where:

$$r=y$$

$$h=3-x=3-y^2$$

hence:

$$dV=2\pi y\left(3-y^2\right)\,dy=2\pi\left(3y-y^3\right)\,dy$$

Adding up all the shells, we get the volume:

$$V=2\pi\int_0^{\sqrt{3}} 3y-y^3\,dy=2\pi\left[\frac{3}{2}y^2-\frac{1}{4}y^4\right]_0^{\sqrt{3}}=\frac{9\pi}{2}$$

Can you try the other axes of revolution now?

 

[stripedcat]

I'm actually totally fine and I know the formulas to do the equations for shell, disk, and washer, and the arc length one as well.

What I'm not so clear on is how to get the values to solve for them unless its rotating around the x-axis as in a.

In this particular case, I can see when going around the y axis, the R, being the larger of two radius, is 3, as that x=3 line is the 'furthest' point from the y-axis that is being rotated around.

My understanding for the r(y) is that since that curve is y=sqrt(x), by solving for y I get y^2 = x, so that's the 'closer' point to the y-axis that is being rotated around.

For c) which is around the x=3 line, in order to get the R(y) value, you are moving to the left (thus, in a negative direction) from the x=3 line until you reach the curve, which we have already established is y^2, so that's where I think the 3-y^2 comes from. r(y) in this case is zero since we're going around the x=3 line

for d) its going around the line x=6, which is +3 from the x=3 line it ends up being (3+3-y^2) or 6-y^2 to find the distance from the x=6 line to the curve.

Is this the correct way of thinking about it?