Shortest distance along the shore and into the lake

[brotherbobby]

Homework Statement

A man is on the shore of a lake at point A and has to get to point B on the lake in the shortest possible time (see Fig below). The distance from point B to the shore is $BC = d$ and the distance $AC=s$. The man can swim in water with a speed of $v_1$ and run along the shore with a speed of $v_2$, greater than $v_1$. Which way should he use - swim from point A straight to B or run a certain distance along the shore and then swim to point B?

Relevant Equations

(1) Pythagorean theorem for a right angled triangle with hypotenuse length $c$ and sides $a,b$ : $c^2=a^2+b^2$
(2) For a function $f(x)$, minimum value of $f$ can be found by solving $\dfrac{df}{dx}=0$. At the minimum, the calculated value of $x$, say some $x_0$, should have $\left.\dfrac{d^2f}{dx^2}\right|_{x=x_0}\!\!\!\!\!\!\!\!\!>0$

Attempt : I copy and paste the problem as it appeared in the text below.

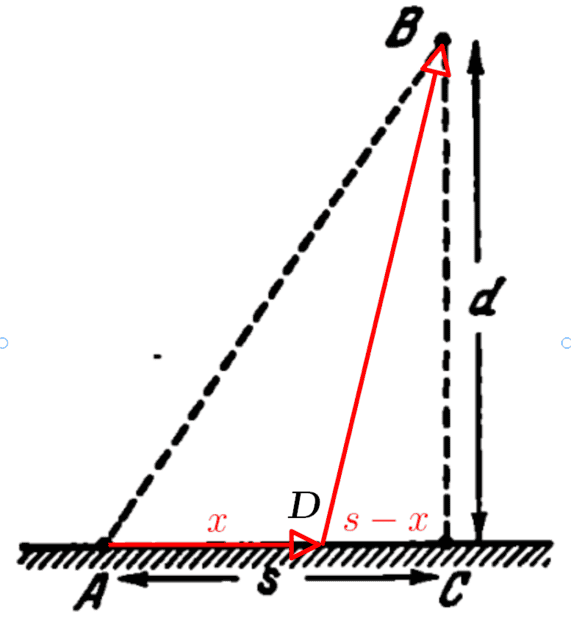To be sure, of course the man cannot swim directly to B for minimum time of travel. He should run a distance ($x$) to some point D along the shore and then swim to B. I draw those details in the diagram to the right.
The time of travel $\small{t=\dfrac{x}{v_2}+\dfrac{\sqrt{d^2+(s-x)^2}}{v_1}}$.
For minimum time, $\small{\dfrac{dt}{dx}=\dfrac{1}{v_2}-\dfrac{s-x}{v_1\sqrt{d^2+(s-x)^2}}=0}$, which, after some elementary algebra, comes out to be $\boxed{\boldsymbol{x=s-\dfrac{v_1d}{\sqrt{v_2^2-v_1^2}}}}\quad{\color{green}{\Large\checkmark}}\qquad(1)$.

I checked for myself that for this value of $x$, $\dfrac{dt^2}{dx^2}>0$

I put the checkmark ($\checkmark$) because the answer checks out with that of the text. Of course the authors have done it without using calculus and that is how one should do it first. I will attempt it presently.

However, if I took values of the different speeds and distances and found out $x$ from equation $(1)$ above, I get a negative answer.

Let the distances and speeds be the following : $s=2\,\text{km}, \, d=6\,\text{km},\, v_1=4\,\text{km/h},\, v_2=8\,\text{km/h}$.

Then from $(1)$, $\small{x=2-\dfrac{4\times 6}{\sqrt{8^2-4^2}}=2-2\sqrt{3}=-\text{ve}\;!}$

This would mean the man should run a distance to the left from A along the shore and then swim to B which cannot be least time. Running the same distance right would lead to a shorter time owing to less distance of swimming.

Request - Where am I going wrong with the numbers?

 

[haruspex]

The thing to check is whether your first equation represents reality in all cases.
For x<0 it doesn't: it gives a negative time for running on the shore.
Consequently, if there is no local minimum with x>0 you get a crazy answer.

 

[brotherbobby]

The thing to check is whether your first equation represents reality in all cases.
For x<0 it doesn't: it gives a negative time for running on the shore.
Consequently, if there is no local minimum with x>0 you get a crazy answer.

Yes, I realise it now. The answer $\boxed{x=s-\dfrac{v_1d}{\sqrt{v_2^2-v_1^2}}}$ makes sense for as long as $x>0$. Put differently, $x=s-\dfrac{v_1d}{\sqrt{v_2^2-v_1^2}}\Rightarrow \dfrac{v_1d}{\sqrt{v_2^2-v_1^2}}=s-x\ge 0$. If however those v's and d's combine to give an s less than x (but s>0), the man should swim directly to A without running along the shore.
As it happened, for the values I took, s turns out to be less than x.

 

[kuruman]

I think your problem was that you measured the "jump in" distance from the starting point. If $x_{opt}$ is the optimum distance from C, the time will be a minimum no matter how far from C the man starts running as long as the starting point is at $s>x_{opt}$. So it makes more sense to optimize $x$ as measured from point C.

Also note that if I define $~~\sin\theta\equiv \dfrac{x}{\sqrt{d^2+x^2}},~~$ where $\theta$ is the angle opposite to right side CD in triangle BCD (see diagram on the right), your equation $$\frac{dt}{dx}=\frac{1}{v_2}-\frac{s-x}{v_1\sqrt{d^2+(s-x)^2}}=0$$becomes $$\frac{1}{v_2}-\dfrac{\sin\theta}{v_1}=0\implies \sin\theta=\frac{v_1}{v_2}.$$ Thus, from the right triangle $$\frac{\sin\theta}{\sqrt{1-\sin^2\theta}}=\tan\theta =\frac{x_{opt}}{d}\implies x_{opt}=\frac{v_1}{\sqrt{v_2^2-v_1^2}}d.$$You might also recognize the path followed by the man as the path of light incident at grazing incidence on a dielectric interface from an optically rarer to an optically denser medium. According to Fermat's principle, when light travels from point A to point B it does so in the least possible time. Angle $\theta$ in this case is the critical angle for total internal reflection.

On edit
I corrected the defining equation of $\sin\theta$ to make it consistent with the text, where it is stated that $\theta$ is the angle opposite to right side CD in triangle BCD and that $x$ is measured from point C. I also added a diagram to make the situation clearer. My thanks to @haruspex for pointing out the inconsistency in post #5. The corrected version does not lead to a solution to the left of A. With the definition of $x$ as the distance from C point A becomes irrelevant. I apologize for the confusion.

 

[haruspex]

If $x_{opt}$ is the optimum distance from C, the time will be a minimum no matter how far from C the man starts running as long as the starting point is at $s>x_{opt}$. So it makes more sense to optimize $x$ as measured from point C.

Also note that if I define $~~\sin\theta\equiv \dfrac{s-x}{\sqrt{d^2+(s-x)^2}},~~$ where $\theta$ is the angle opposite to right side CD in triangle BCD, your equation $$\frac{dt}{dx}=\frac{1}{v_2}-\frac{s-x}{v_1\sqrt{d^2+(s-x)^2}}=0$$becomes $$\frac{1}{v_2}-\dfrac{\sin\theta}{v_1}=0\implies \sin\theta=\frac{v_1}{v_2}.$$ Thus, from the right triangle $$\frac{\sin\theta}{\sqrt{1-\sin^2\theta}}=\tan\theta =\frac{x_{opt}}{d}\implies x_{opt}=\frac{v_1}{\sqrt{v_2^2-v_1^2}}d.$$

Neat, but it would still have led to an answer that the place to jump in is to the left of A. I would guess @brotherbobby would have been just as puzzled.
Either way, the resolution of the puzzlement is that the time of travel is $\small{t=\dfrac{|x|}{v_2}+\dfrac{\sqrt{d^2+(s-x)^2}}{v_1}}$.

 

[Hill]

Either way, the resolution of the puzzlement is that the time of travel is $\small{t=\dfrac{|x|}{v_2}+\dfrac{\sqrt{d^2+(s-x)^2}}{v_1}}$.

Also, $x$ should be redefined: instead of

a distance (x)

(which is positive by definition) it is a coordinate of $D$ with the origin in $A$.

 

[kuruman]

Neat, but it would still have led to an answer that the place to jump in is to the left of A. I would guess @brotherbobby would have been just as puzzled.
Either way, the resolution of the puzzlement is that the time of travel is $\small{t=\dfrac{|x|}{v_2}+\dfrac{\sqrt{d^2+(s-x)^2}}{v_1}}$.

I messed up the definition of $\sin\theta$ because I copied and pasted from @brotherbobby's expression without changing $s-x$ to $x$ in the numerator. The original equation is inconsistent with the text. See edit note and added figure in post #4. Thanks for the catch.