Show that the series ##\sum_{n=2}^\infty\dfrac {1}{n^2\ln (n)}##converges

[chwala]

Homework Statement

see attached.

Relevant Equations

knowledge of series and convergence/divergence

This is the question,

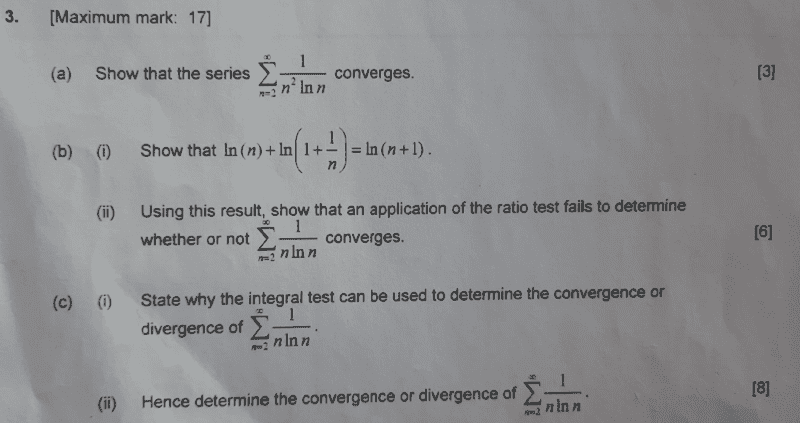
its long since i studied convergence...I need to attempt all the questions (attached)i will therefore make an attempt to answer one part at a time i.e $a$ first.

wawawawawa! does not look nice...let me look at my old notes on this chapter then i will respond later...give me time.

*I need to find the formula for this series...

 

[BvU]

Hi ,

Don't be intimidated! If something can be shown to be smaller than the terms in a series that you know converges, you are done. You don't need 'the formula' for such a series.

$\$

 

[fresh_42]

Do you know something about $\sum_{n=1}^\infty \dfrac{1}{n^2}$?

 

[chwala]

Do you know something about $\sum_{n=1}^\infty \dfrac{1}{n^2}$?

It should be convergent by using Comparison Test...sorry i am held up a bit...i will look at this in a few hours...cheers Fresh.

 

[chwala]

Hi ,

Don't be intimidated! If something can be shown to be smaller than the terms in a series that you know converges, you are done. You don't need 'the formula' for such a series.

$\$

Nice...i was thinking along the lines of finding the formula of the series then establish its limit as n tends to infinity...

I will look at the approach suggested by Fresh...

 

[BvU]

Google is your friend ! I never heard of the Basel problem, but thanks to you I now bumped into it. Thanks !
(and idem Parseval's theorem...)

$\$

 

[Mark44]

It should be convergent by using Comparison Test

There is also the concept called "p - series," usually the subject of a theorem/test of the same name. It says that the series $\sum_{n=1}^\infty \frac 1 {n^p}$ converges if p > 1, and diverges if $0 < p \le 1$.

Nice...i was thinking along the lines of finding the formula of the series then establish its limit as n tends to infinity...

But that isn't what is asked for. The problem asks only whether the given series converge or diverge. Finding the sum of a (convergent) series is a different matter.

 

[chwala]

Can i use the squeeze theorem? i.e by finding two convergent series, $\dfrac{-1}{n^2}$ and $\dfrac{1}{n^2}$
We shall have,
$\dfrac{-1}{n^2}≤\dfrac{1}{n^2⋅\ln(n)}≤\dfrac{1}{n^2}$
Since the two given series are convergent to zero, then it also follows that, $\dfrac{1}{n^2⋅ln(n)}$ converges.

 

[chwala]

Using the Basel approach, we think of a series and we try and determine whether it's sum converges...
Consider the series;
$\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}$
$\dfrac{1}{n^2}$≤$\dfrac{1}{n(n-1)}$=$\dfrac{1}{n-1}-\dfrac{1}{n}$ for $n≥2$
$S_n$=$\sum_{k=2}^n\dfrac {1}{k^2}$≤$\sum_{k=2}^n$$\dfrac{1}{k-1}-\dfrac{1}{k}$=$1-\dfrac{1}{n}≤1$
Since the sum converges and is upper bounded then it follows that our series, $\sum_{n=2}^\infty\dfrac {1}{n^2\ln (n)}$ is convergent.

 

[fresh_42]

Can i use the squeeze theorem? i.e by finding two convergent series, $\dfrac{-1}{n^2}$ and $\dfrac{1}{n^2}$
We shall have,
$\dfrac{-1}{n^2}≤\dfrac{1}{n^2⋅ln(n)}≤\dfrac{1}{n^2}$
Since the two given series are convergent to zero, then it also follows that, $\dfrac{1}{n^2⋅ln(n)}$ converges.

The sums converge to $-\pi^2/6$ which is why the term in the middle converges, too. Btw., you could have chosen $0$ on the left-hand side. E.g. $1/n\leq 1/n \leq 1/n$ and everything converges to zero, but none of it as a sum.

Therefore it remains to show that $\sum 1/n^2$ converges.

 

[chwala]

The sums converge to $-\pi^2/6$ which is why the term in the middle converges, too. Btw., you could have chosen $0$ on the left-hand side. E.g. $1/n\leq 1/n \leq 1/n$ and everything converges to zero, but none of it as a sum.

Therefore it remains to show that $\sum 1/n^2$ converges.

Thanks...yap I got mixed up on...limit of the sequence with sum of a series ...

 

[chwala]

I will proceed with the questions. For part $b(i)$ we want to show that;
$\ln (n)+\ln(1+\dfrac {1}{n})= \ln (n+1)$

Using the property,
$\ln A + \ln B= \ln (A⋅B)$
lhs becomes,
$\ln \dfrac {n(n+1)}{n}$=$\ln(n+1)$ which is the same as the rhs.

For part $b(ii)$,
$$\lim_{n→∞}|\dfrac {U_{n +1}}{U_n}|=\lim_{n→∞} \ln\left [ (n+2)- \dfrac {n(n+1)}{n}\right]
=\lim_{n→∞} \ln\left [\dfrac{n(n+2)-n(n+1)}{n}\right]$$
=$$\lim_{n→∞} \ln\left [\dfrac{n^2+2n-n^2-n}{n}\right]
=\lim_{n→∞} \ln\left [\dfrac{n}{n}\right]
=\lim_{n→∞} \ln [1]=1$$
Therefore the ratio test fails to determine convergence of the given series.

 

[docnet]

$Lim_{n→∞} ln [1]=1$

$\ln(1)=0$

 

[chwala]

True, slight mix up...cheers docnet ...

At times it happens you solve a very long math problem then end up making a mix up...happens to me when my brain is really thinking...then oops ...$2x=5$, solving for $x$ and I say $x=\frac {2}{5}$ wah!

 

[chwala]

Something wrong with my ratio test post $12$.
If $$\lim_{n→∞}\left|\dfrac {U_{n +1}}{U_n}\right|=0<1$$ implies Convergence...

Can i say, =$\lim_{n→∞} \ln\left [\dfrac{n}{n}\right]= \left[\dfrac{∞}{∞}\right]=1$...implying that ratio test is inconclusive as expected. ...still looks wrong as i have left out the natural log...

 

[docnet]

Can i say, =$Lim_{n→∞} ln [\dfrac{n}{n}]= [\dfrac{∞}{∞}]=1$...implying that ratio test is inconclusive as expected. ...still looks wrong as i have left out the natural log...

L'Hôpital's rule can be used to evaluate limits of indeterminate forms. It's a standard calculus trick, though it doesn't seem like you need it for this problem.

 

[BvU]

For part b(ii),
$$Lim_{n→∞}|\dfrac {U_n +1}{U_n}|=Lim_{n→∞} ln[ (n+2)- \dfrac {n(n+1)}{n}]$$

First of all: you want to use \lim and \log (or, if an engineer, \ln ) :$$
\lim_{n→∞}|\dfrac {U_n +1}{U_n}|=\lim_{n→∞} \ln[ (n+2)- \dfrac {n(n+1)}{n}]
$$second: you want to use \left [ and \right ] as well as \left | and \right | : $$
\lim_{n→∞}\left |\dfrac {U_n +1}{U_n}\right |=\lim_{n→∞} \ln\left [ (n+2)- \dfrac {n(n+1)}{n}\right ] \tag {C1}$$

For even more control:

The advantage of \left and \right is that they grow to any size to fit the need. But on some occasion you may want to set your own larger size. One way to do this is to use the big commands:
\big, \bigl, \bigm, \bigr,
\Big, \Bigl, \Bigm, \Bigr,
\bigg, \biggl, \biggm, \biggr,
\Bigg, \Biggl, \Biggm, \Biggr

So much for today's ##\LaTeX# lesson .

Then: it's a good habit to explain newly introduced symbols. I don't know what you mean with the symbol $U_n$ in post #12. My best guess is $$U_n \equiv \sum_{k=2}^n \frac 1 {k\log k} $$but then I really don't know what you want with $U_n + 1$. A typo and you mean $U_{n+1}$ ? But that doesn't explain to me how $n+2$ pops up in $(C1)$.

Finally: did you notice @fresh_42 post #10 ? It means we are not finished with part (a) yet !

$\$

 

[chwala]

Ok i think i got it in a different way, check this out,

Let $U_n$= $\dfrac{1}{n\ln(n)}$
$U_{n+1}=\dfrac{1}{(n+1)\ln(n+1)}$
$\lim_{n→∞}\left|\dfrac {U_n +1}{U_n}\right|=\lim_{n→∞} \dfrac{1}{(n+1)\ln(n+1)}⋅$$\dfrac{n\ln(n)}{1}$
$=\lim_{n→∞}\left [\dfrac{n}{(n+1)}\right]⋅\lim_{n→∞}\ln\left[\dfrac{n}{(n+1)}\right]$
we know that $\lim_{n→∞} \ln\left[\dfrac{n}{(n+1)}\right]=1$ therefore,
$=\lim_{n→∞}\left [\dfrac{n}{(n+1)}\right]$=$\lim_{n→∞}\left [\dfrac{1}{(1+1/n}\right]$=$\left[\dfrac{1}{(1+0}\right]=1$
This is inconclusive for the ratio test.

 

[BvU]

Ok, provided you mean $U_{n+1}$, not $U_n+1\ \$ !

So $U_n$ is not the sum, but the term. I should have guessed .

Don't forget the $\TeX$ lesson! $nln$ looks ugly !$\$

 

[fresh_42]

Finally: did you notice @fresh_42 post #10 ? It means we are not finished with part (a) yet !

I noticed post #9 now which made my post #10 obsolete. I didn't notice at the time when I answered post #8. My fault.

 

[BvU]

I noticed post #9 now which made my post #10 obsolete. I didn't notice at the time when I answered post #8. My fault.

No need to apologize -- I just wanted to make clear (rub in ) we are basing our result on Euler's.

$\$

 

[BvU]

$$=Lim_{n→∞} [\dfrac{n}{(n+1)}]⋅ln[\dfrac{n}{(n+1)}]$$

Does this look like you think $${\log a\over \log b} = \log {a\over b} \quad ? $$

$\$

 

[chwala]

Ok, provided you mean $U_{n+1}$, not $U_n+1\ \$ !

So $U_n$ is not the sum, but the term. I should have guessed .

Don't forget the $\TeX$ lesson! $nln$ looks ugly !$\$

I will amend ...

 

[chwala]

Does this look like you think $${\log a\over \log b} = \log {a\over b} $$

$\$

Seen that...let me recheck my steps by tomorrow in that case it would be prudent to use L' Hopital's rule...cheers let's see how it goes...

 

[SammyS]

Seen that...let me recheck my steps by tomorrow in that case it would be prudent to use l' hopital rule...cheers let's see how it goes...

To be more direct.

$\dfrac{\ln(a)}{\ln(b)}\ne\ln\left(\dfrac a b \right)$

 

[chwala]

$U_n$= $\dfrac{1}{n\ln(n)}$
$U_{n+1}=\dfrac{1}{(n+1)\ln(n+1)}$
$$\lim_{n→∞}|\dfrac {U_n +1}{U_n}|=\lim_{n→∞}\left[ \dfrac{1}{(n+1)\ln(n+1)}⋅\dfrac{n\ln(n)}{1}\right]
=\lim_{n→∞} \left[\dfrac{n}{(n+1)}]⋅[\dfrac{\ln n}{(\ln(n+1)}\right]$$
on applying L' Hopital's rule and differentiation we have,
$$\lim_{n→∞}\left[\dfrac{(n+1)1-n(1)}{(n+1)^2}⋅\dfrac{\ln n}{\ln(n+1)}\right]+\lim_{n→∞}\left[\dfrac{n}{n+1}⋅\dfrac{n+1}{n}\right]$$
$$\lim_{n→∞}\left[\dfrac{1}{(n+1)^2}\right]⋅\lim_{n→∞}\left[\dfrac{\ln n}{(\ln(n+1)}\right]+\lim_{n→∞}1$$
we know that $$\lim_{n→∞} \left [\dfrac{\ln (n)}{\ln(n+1)}\right]=1$$ therefore
$$\lim_{n→∞}\left[\dfrac{1}{(n^2+2n+1)}\right]⋅1+1=0⋅1+1=1$$ The ratio test is inconclusive.

 

[docnet]

$=\lim_{n→∞} [\dfrac{n}{(n+1)}]⋅[\dfrac{\ln n}{(\ln(n+1)}]$

You might want to use the property $$\displaystyle{\lim_{n \to \infty}} a\cdot b\quad=\quad\displaystyle{\lim_{n \to \infty}} a \cdot \displaystyle{\lim_{n \to \infty}} b$$

on applying hopital rule and differentiation we have,
$\lim_{n→∞}[\dfrac{(n+1)1-n(1)}{(n+1)^2}]⋅[\dfrac{\ln n}{(\ln(n+1)}]+[\dfrac{n}{n+1}]⋅[\dfrac{n+1}{n}]$

Using L'hôpital's rule looks like:
$$\displaystyle{\lim_{n \to \infty}} \frac{f}{g} \quad = \quad \displaystyle{\lim_{n \to \infty}} \frac{f'}{g'}$$

 

[Mark44]

The ratio test is inconclusive.

Which is what the problem statement asked you to verify.

Your work in the previous post, #26, is more involved than it needs to be.

$\lim_{n→∞} [\dfrac{n}{(n+1)}]⋅[\dfrac{\ln n}{(\ln(n+1)}]$

You don't need to use L'Hopital on the whole thing, but can get by applying it to the latter factor $\frac{\ln(n)}{\ln(n + 1)}$.
It's easy to prove that $\lim_{n \to \infty} \frac n {n + 1} = 1$, so if you can show that the limit of the ln expression exists, then you have found the limit of the larger expression.

 

[chwala]

That is what I used...though not indicated in working ...

You might want to use the property $$\displaystyle{\lim_{n \to \infty}} a\cdot b\quad=\quad\displaystyle{\lim_{n \to \infty}} a \cdot \displaystyle{\lim_{n \to \infty}} b$$

Using L'hôpital's rule looks like:
$$\displaystyle{\lim_{n \to \infty}} \frac{f}{g} \quad = \quad \displaystyle{\lim_{n \to \infty}} \frac{f'}{g'}$$

 

[chwala]

I will look at part (c) later...cheers