Showing that operators follow SU(2) algebra

[graviton_10]

For two quantum oscillators, I have raising and lowering operators

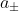and

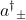, and the number operator

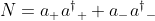. I need to check if operators below follow

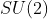commutation relations.

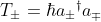
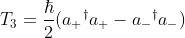
Now as far as I know, SU(2) algebra commutation relation is [T_1, T_2] = i ε^ijk T_3. So, should I just get T_1 and T_2 in terms of T_- and T_+ and then try to check if I get they follow the SU(2) commutation relation?

 

[fresh_42]

If it helps you can find the basis transformations here (also those to the Pauli matrices):
https://www.physicsforums.com/insights/journey-manifold-su2-part-ii/

There we have $N=H, T_+=X, T_-=Y$ and $T_1=U,T_2=V,T_3=W.$

 

[martinbn]

Just a pedantic comment but $SU(2)$ is a group, and $\mathfrak{su}(2)$ is an algebra.