Simple Counter-balance/Counter-weight Calculation Problem

[rh2022]

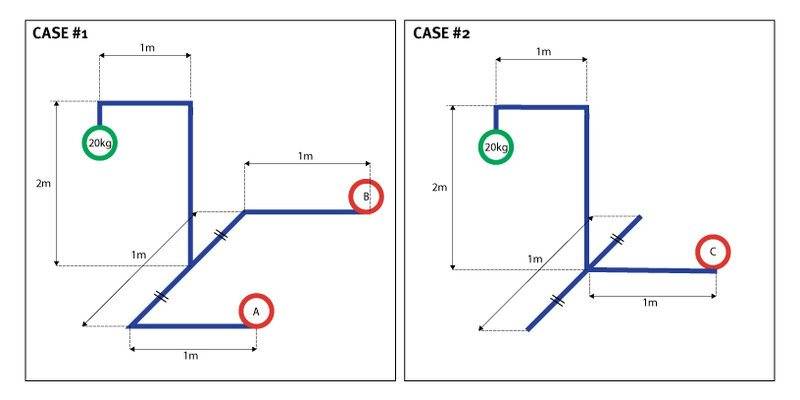
Hi, I am trying to figure out how much weight is needed to counter balance a pole stand where an object(m kg) is hanging. I also want to know which is more effective way to place counterweight as shown in the picture below. I was wondering if the counterweight A, B, and C are equal.

It seems to be a simple torque problem, but I am a bit confused as the pole is not a straight line.
Any help would be appreciated.

 

[Baluncore]

Welcome to PF.
It is a simple torque problem.
Map all the mass onto the horizontal plane.
Assume the pole frame is rigid and has no mass.
Assume the diagonal line is the fulcrum = hinge line.
Case #1: A = B = 10 kg. A + B = 20 kg.
Case #2: C = 20 kg.

 

[rh2022]

Thank you for your reply.
I have an additional question.

What if the pole frame has mass: pole frame = 50kg, pole arm = 30kg, base frame = 20kg, base legs = 20kg each. Does it make difference?
I want the green object X(20kg) rotate/swing 360 degree around the Pole Frame without flipping it.
Do you think both Case #1 and Case #2 should provide stable support if I place a 20kg+ counter weight at the end base leg frame?

 

[Baluncore]

I want the green object X(20kg) rotate/swing 360 degree around the Pole Frame without flipping it.

You must draw the plan view, then mark all the centres of mass.
Identify the possible fulcrum line for each situation.
From that you can work out the total torque for different rotation angles.
You are considering only the static balance, do not spin it rapidly.
Note that when it starts to overbalance it will accelerate rapidly.

I expect case #2 will fail at some angle well before 135°.
Case #1 may be more secure, but you must do the numbers.