Dylan.Wallett
- 4
- 0
Homework Statement
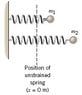
The drawing shows a top view of a frictionless horizontal surface, where there are two springs with particles of mass*m1*and*m2*attached to them. Each spring has a spring constant of*120*N/m. The particles are pulled to the right and then released from the positions shown in the drawing. How much time passes before the particles are side by side for the first time at*x*= 0 m if the following masses are used: m1 = 3.0 kg m2 = 2.7 kg
Homework Equations
w = squ root k/m - frequency of vibration
w = 2 pi/T
E=1/2mv^2 + 1/2kx^2
The Attempt at a Solution
I am pretty stumped with this one. I feel we need to know the distance that the two particles were pulled to and then released.
I started with
m1 - w= squ root k/m
= squ root 120/3.0
= 2.0 rad/s
m2 - w= squ root k/m
= squ root 120/2.7
= 2.1 rad/s
Thanks