Simple Linkage with Reciprocating points

[mtommis]

TL;DR Summary: Anybody help me get my head around this please

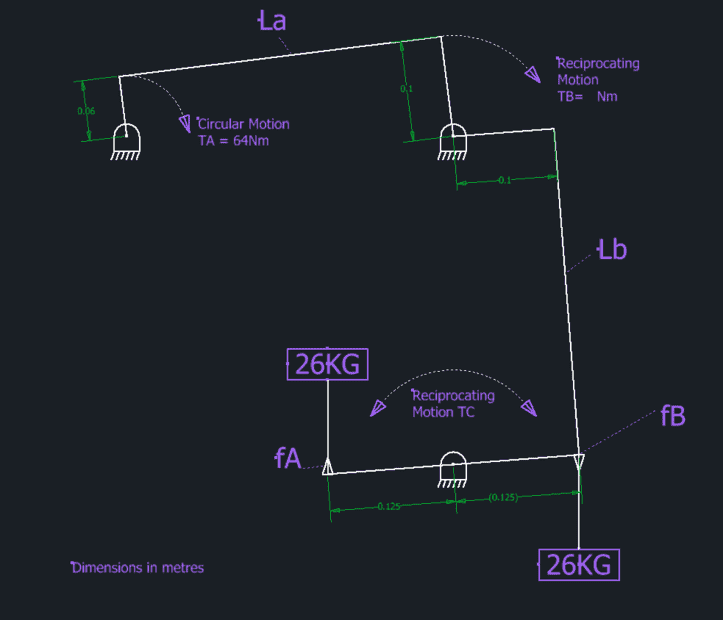
Hi, If anybody could give me a steer on solving this that would be great.

I am trying to solve the maximum forces at points fA and fB
If the force from the drive TA = 64/0.6 = 1066.666N
Point TB has equal arms so the same force goes through to Lb

Not quite sure how to resolve the final bit though

 

[erobz]

1) Is the linkage assumed to be effectively massless?

2) You are looking for the maximum forces developed at $f_A$ and $f_B$ over the entire range of motion?

3) Beyond the diagram and the driving torque what have you figured out?

 

[Baluncore]

Most of the mechanism appears to be redundant.
The point B is being driven sinusoidally, through ±0.06, indirectly through La and Lb, by crank TA.

 

[mtommis]

Hi,

Thanks for taking the time to reply

Yes, I am not considering the mass of the linkage at this time and am only interested in determining the maximum force developed at fA and fB.

The current arrangement is using a rotating motor at point TA and the various linkages supply force to drive the reciprocating motion at point Tc - overly complicated to translate moition horizontally and then vertically around a corner to the end drive position.

I am trying to workout the forces at fA and fB with the goal of replacing the motor and linkages with 2 linear actuators. I am assuming the 26kg (255N) imposed loads will effectivly negate each other. although they operate on different strokes of the actuator (extension and retraction)
I know the existing motor supplies 64Nm of torque and that is sufficient to drive the linkage but that may have surplus capacity which can be designed out.

 

[Lnewqban]

Welcome, @mtommis !

Have you considered the angular velocity and inertia of that system of masses?
Are those affected by gravity forces?

 

[erobz]

Most of the mechanism appears to be redundant.
The point B is being driven sinusoidally, through ±0.06, indirectly through La and Lb, by crank TA.

As a mere mortal I made a parametric model and spun it around (seems legit). How did you conclude that?

 

[erobz]

Anyhow, I wonder what we are supposed to assume is going on with this motor? Is it rotating the link $TA$ at constant angular velocity, or is it supplying a constant torque, or neither? My gut is telling me neither.

 

[Baluncore]

How did you conclude that?

I felt, by inspection, that it was the obvious result.
Back thinking it, my analysis went like this:
Circular motion TA drives crank through amplitude ±0.06 ;
That moves link La, axially through ±0.06 ;
The double crank TB has length 0.1; so cannot rotate, must reciprocate ±0.06 ;
The double crank has equal input and output radius, so output is ±0.06 ;
That moves link Lb, axially through ±0.06 ;
Which drives the point of fB through ±0.06 ;
Since the lengths of La and Lb appear great, direction is not critical,
and since all angles operate about 90°, there is no amplitude gain change,
so there will be some symmetric→odd harmonic distortion of reciprocation,
but amplitude will remain sinusoidal, at about ±0.06 ;
Was I wrong?

 

[erobz]

Was I wrong?

Not from what I can tell.

 

[erobz]

I don't know if you are still interested, but finding $\beta$ as a function of $\theta$, is turning out to be an absolute bear of a trig problem, unless I'm under thinking it...

Even still, once you do that, you have to get derivatives $\dot \beta$, and $\ddot \beta$ if you hope to find the accelerations of the lower rocker.

Maybe I'm missing something obvious about having the approximate amplitude?

 

[Baluncore]

Not quite sure how to resolve the final bit though

64 Nm on the crank arm of length 0.06 = 1067 N axial force in the linkage.
That movement, and therefore the force, appear unchanged at point A or B.
The length of the rocking arm on a fulcrum between A and B is not important.
Therefore, fA or fB = 1067 N.
That is the force that must be delivered by the linear activator.

 

[erobz]

64 Nm on the crank arm of length 0.06 = 1067 N axial force in the linkage.
That movement, and therefore the force, appear unchanged at point A or B.
The length of the rocking arm on a fulcrum between A and B is not important.
Therefore, fA or fB = 1067 N.
That is the force that must be delivered by the linear activator.

I have doubts about this motor is actually supplying a constant torque, the load is varying quite dramatically over a cycle?

Either way, I think the OP would be better served by just figuring out what the lower rocker is supposed to do, and spec a linear actuator for that action as opposed to figuring out what the linkage that is being replaced does. IMO.

 

[Baluncore]

I have doubts about this motor is actually supplying a constant torque, the load is varying quite dramatically over a cycle?

Any simple crank has a cyclic load, with two zeros, so that sinusoidal variation must be the case.

Either way, I think the OP would be better served by just figuring out what the lower rocker is supposed to do, and spec a linear actuator for that action as opposed to figuring out what the linkage that is being replaced does. IMO.

You are assuming the peak power is certainly known from the geometry. I advise caution. The original designer satisfied the requirements. The motor provided does the job now without failure or complaint. We cannot tell if the motor size was doubled at some stage, to overcome an unusual situation. During starting, from static to dynamic, or if the varying material load sometimes exceeds the estimated 26 kg, then more power will occasionally be needed.

The motor and linkage should be replaced with something that can provide an equal or a greater force. If less force is needed, then power consumed will be less than the maximum.

Is there a shear pin in the existing system? How will that protective feature be implemented with the new linear actuator? What will break?

 

[erobz]

The motor and linkage should be replaced with something that can provide an equal or a greater force. If less force is needed, then power consumed will be less than the maximum.

My only gripe would be the forces required now are through a potentially “lossy” linkage with inertial characteristics that we know little about and will not be present in the redesign.