Simple pendulum with moving support

[member 731016]

Homework Statement

I am trying to find the coordinates of a simple pendulum on a rotating support.

Relevant Equations

Please see below.

For this problem,

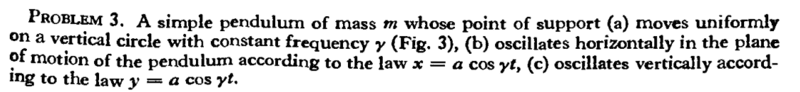
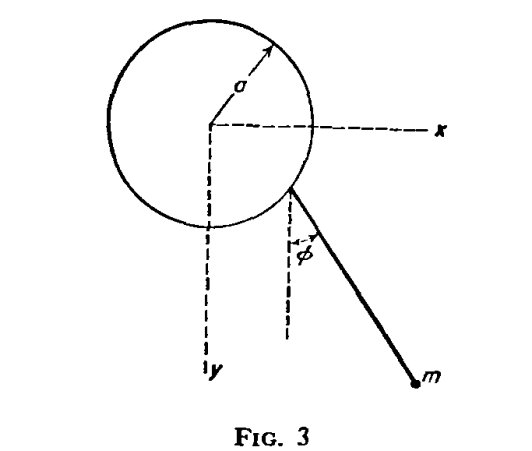
The correct coordinates are,

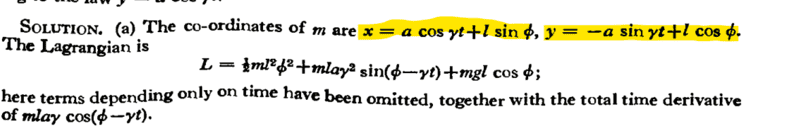
However, I am confused how they got them.

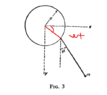
So here is my initial diagram. I assume that the point on the vertical circle is rotating counterclockwise, that is, it is rotating from the x-axis to the y-axis.

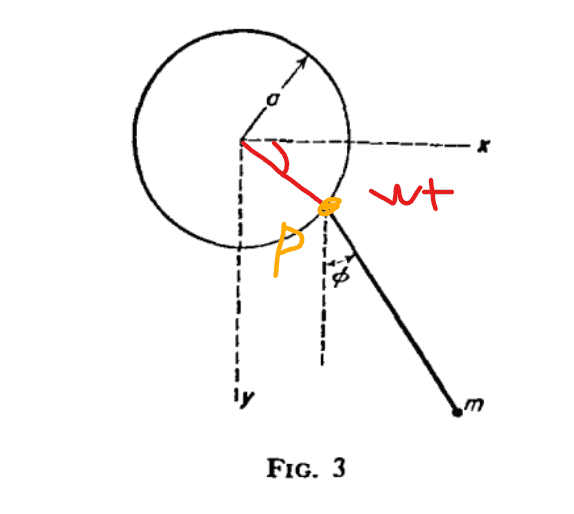
Thus $\omega t > 0$ for the point. i.e angle subtended from positive x-axis to positive y-axis is positive. However, this does not give the correct relations for the point.

To get the correct relations, you must make the diagram,

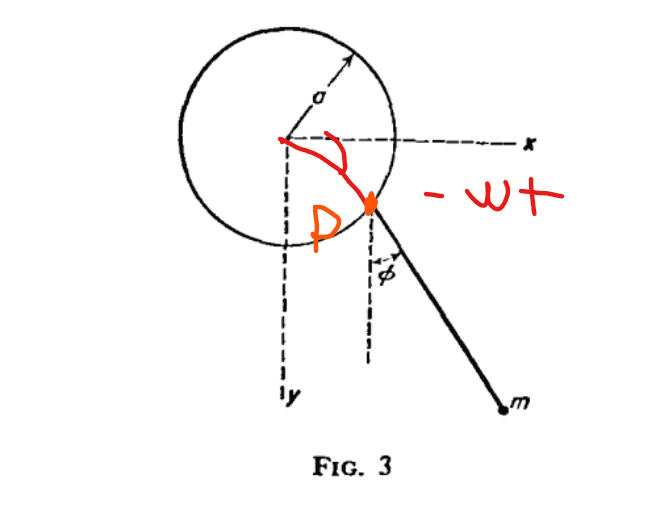
Due to the odd and even function properties of sine and cosine, this gives the desired solution since $$-\omega t < 0$$. However, does anybody please know what convention this is called, i.e. angle $$\omega t$$ rotated from the positive x-axis to the negative y-axis is positive?

Thanks for any help!

 

[haruspex]

The question does not specify whether the rotation is clockwise or anticlockwise. If it is anticlockwise then the diagrammed position can be thought of as being with t negative.

 

[member 731016]

The question does not specify whether the rotation is clockwise or anticlockwise. If it is anticlockwise then the diagrammed position can be thought of as being with t negative.

Thank you for your reply @haruspex!

If the question does not specify the direction of rotation, is it in general safe to assume that is it anticlockwise, from the positive x-axis to the positive y-axis?

This question is from landau mechanics 3rd edition page 11, problem 3.

Thanks!

 

[haruspex]

Thank you for your reply @haruspex!

If the question does not specify the direction of rotation, is it in general safe to assume that is it anticlockwise, from the positive x-axis to the positive y-axis?

If x is to the right and y is up then yes, but here the positive y axis is down, so all bets are off.

 

[kuruman]

If the question does not specify the direction of rotation, is it in general safe to assume that is it anticlockwise, from the positive x-axis to the positive y-axis?

The question indeed does not specify the sense of the rotation. However, in order to write equations and solve the problem, one is free to choose but must choose a sense of rotation. The author of the solution has chosen
$x(t)=a\cos\!\gamma t~\implies \dot x(t)=-\gamma a \sin\!\gamma t$
$y(t)=-a\sin\!\gamma t~\implies \dot y(t)=-\gamma a \cos\!\gamma t$
It follows that
$x(0)=a~;~~ \dot x(0)=0$
$y(0)=0~;~~ \dot y(0)=-\gamma a$
Conventionally assuming that $\gamma$ represents an angular speed not an angular velocity, we see that at $t=0$ the point of support is on the positive x-axis moving in the negative y-direction, i.e. "up" in the original Figure 3. Thus, the author of the solution implicitly chose the rotation to be counterclockwise by specifying $x(t)$ and $y(t)$.

We can interpret the original Figure 3 as showing the point of support at time $t$ such that $~\frac{3}{2}\pi < \gamma t < 2\pi$. Your first modified Figure 3 would be correct if you labeled the "larger angle" as $\gamma t.$