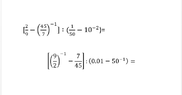Alexstrasuz1
- 20
- 0
If its not problem for you to check these last two. I got no more of these.
If you have some kind a book with tasks like this on internet I would love to print it out so I can have some fun.
View attachment 3008
1ST answer 20/3
2ND answer -20/3
If you have some kind a book with tasks like this on internet I would love to print it out so I can have some fun.
View attachment 3008
1ST answer 20/3
2ND answer -20/3