Sliding a cloth beneath a block causing tipping

[annamal]

TL;DR Summary

If a cloth were slid underneath a block and we take the moment about the tipping point (normal force), why is there no force counteracting the moment from the weight of the block? If we take the moment about the center of gravity, there is the frictional force and normal force countering each other's moments though.

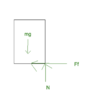
For this freebody diagram showing a cloth being pulled from underneath a block, if we take the moment about the normal force:
m*g*L/2 = 0, there is no force counteracting the moment from the weight of the block.

But if we take the moment about the center of gravity:
N*L/2 - Ff*H/2 = 0

How do you explain the fact that taking the moment about the normal force (tipping point) has no force to counteract the moment from the weight of the block?

 

[Lnewqban]

For the FBD to be true, some horizontal force acting on the CM should be compensating Ff.
Otherwise, the block would tend to rotate CCW, making N to relocate itself to the left bottom edge.

 

[annamal]

For the FBD to be true, some horizontal force acting on the CM should be compensating Ff.
Otherwise, the block would tend to rotate CCW, making N to relocate itself to the left bottom edge.

View attachment 347789

The fbd is for a cloth sliding out from the bottom of the block.
If the block rotates ccw, shouldn’t the normal force be on the bottom right of the block instead?
Correction: If the block rotates ccw, the normal force should be the bottom left of the block.

This doesn’t answer my question that if I take the moment about the normal force location, what force counteracts the the moment from the force of gravity though?

 

[Lnewqban]

The fbd is for a cloth sliding out from the bottom of the block.

From right to left, I assume.

This doesn’t answer my question that if I take the moment about the normal force location, what force counteracts the moment from the force of gravity though?

We are trying to answer your question together

 

[annamal]

From right to left, I assume.



We are trying to answer your question together

Yes there is a cloth sliding from under the block from right to left

 

[Lnewqban]

The fbd is for a cloth sliding out from the bottom of the block. If the block rotates ccw, shouldn’t the normal force be on the bottom right of the block instead?

The fbd represents a cloth sliding, from right to left, out from the bottom of the block, which is tending to rotate CW, as represented.

Assuming the N force was initially located directly under the weight vector, what made it move to the right corner?

If, for any reason, the block instead rotates CCW, shouldn’t the normal force be on the bottom left edge of the block instead?

 

[Lnewqban]

Yes there is a cloth sliding from under the block from right to left.

... and there is a linear inertial resistance of the mass of that block to that forced (Ff) sliding movement.
There is also a rotational inertia inertial resistance of the block to the induced moment and tipping.

 

[berkeman]

For the FBD to be true, some horizontal force acting on the CM should be compensating Ff.

Nice kiss! Is that your girlfriend? (Oh, maybe I should not have asked that...)

 

[annamal]

For the FBD to be true, some horizontal force acting on the CM should be compensating Ff.

If I slide a cloth from right to left underneath a block, what is the compensating horizontal force on the CM?

Otherwise, the block would tend to rotate CCW, making N to relocate itself to the left bottom edge.

Are you saying that sliding a cloth underneath the block would make it rotate ccw?

 

[Lnewqban]

If I slide a cloth from right to left underneath a block, what is the compensating horizontal force on the CM?

Please, see post 7.
Please, note that the CM of the braking motorcycle shown in post 2 is not located directly over the front wheel.

Are you saying that sliding a cloth underneath the block would make it rotate ccw?

Only if sliding it from left to right.

 

[annamal]

I am thinking about this and wondering whether the drag force is what causes the block to tip, so in a vacuum, if you slide a cloth underneath the block from right to left, there should be no tipping.

 

[A.T.]

... so in a vacuum, if you slide a cloth underneath the block from right to left, there should be no tipping.

No, it could tip over in vacuum too.

How do you explain the fact that taking the moment about the normal force (tipping point) has no force to counteract the moment from the weight of the block?

Because the rate of angular momentum change (= net moment) depends on the choice of reference point. The horizontal linear acceleration of the center of mass constitutes a change of angular momentum around every reference point that is not on the horizontal line through the center of mass (like the tipping edge), so there is no reason to expect net zero moment around such a point.

 

[annamal]

Because the rate of angular momentum change (= net moment) depends on the choice of reference point. The horizontal linear acceleration of the center of mass constitutes a change of angular momentum around every reference point that is not on the horizontal line through the center of mass (like the tipping edge), so there is no reason to expect net zero moment around such a point.

Could you explain that in simpler terms please? I get the angular momentum change = net moment. But then got lost afterwards. I am looking at the block in terms of statics though and you seem to be talking about it in terms of dynamics?

 

[A.T.]

Could you explain that in simpler terms please?

See Figure 6.1.1c here:
https://phys.libretexts.org/Courses...ntum/6.1:_Linking_Linear_and_Angular_Momentum

What applies to the point particle there, also applies to the center of mass of the block. And if the magnitude of the linear velocity changes, then so does the angular momentum around that reference point shown there.

I am looking at the block in terms of statics though and you seem to be talking about it in terms of dynamics?

In the inertial reference frame the block is accelerating horizontally due to the frictional force. To make it static you would have to adopt an non-inertial reference frame, which involves inertial forces and moments.