Small bead - Circular loop Problem

Just use the standard equations for uniformly accelerated motion. ...In summary, a small bead is fixed on a circular loop of radius R and the loop is rotating about axis YY' with constant angular acceleration alpha. The loop starts from rest and the acceleration of the bead at any instant 't' can be determined using the angular acceleration equation.
  • #1
Albinjijo
Homework Statement
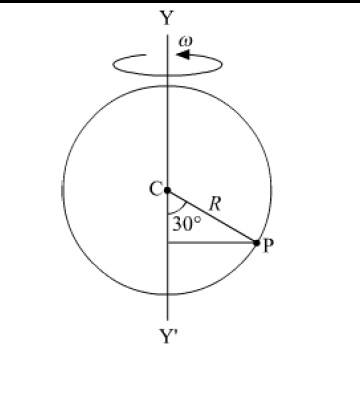
A small bead is fixed on a circular loop of radius R as shown in the figure below. The
loop is rotating about YY axis with constant angular acceleration ‘α’. The loop starts
from rest, then, the bead is in circular motion, then acceleration of the bead at instant
‘t’ is_______.
Relevant Equations
Angular Acceleration equation
Homework Statement: A small bead is fixed on a circular loop of radius R as shown in the figure below. The
loop is rotating about YY axis with constant angular acceleration ‘α’. The loop starts
from rest, then, the bead is in circular motion, then acceleration of the bead at instant
‘t’ is_______.
Homework Equations: Angular Acceleration equation

2-1.jpg

2.jpg


MY ATTEMPT

3.jpg
3-1.jpg
 
Physics news on Phys.org
  • #2
Hello. Welcome to PF!
Albinjijo said:
Homework Statement: A small bead is fixed on a circular loop ...

If I'm interpreting the problem correctly, then the bead cannot slide along the loop. It is fixed at point P. So, I think this is just a kinematics problem. No need to consider forces.
 

FAQ: Small bead - Circular loop Problem

What is the "Small bead - Circular loop Problem"?

The "Small bead - Circular loop Problem" is a physics problem that involves a small bead sliding along a circular loop. It is commonly used as an example in introductory physics courses to demonstrate the application of Newton's laws of motion.

What are the forces acting on the bead in the "Small bead - Circular loop Problem"?

The forces acting on the bead in this problem are the tension force from the string, the weight force due to gravity, and the normal force from the loop. These forces must be balanced for the bead to maintain circular motion.

How is the speed of the bead related to the radius of the loop in the "Small bead - Circular loop Problem"?

The speed of the bead is directly related to the radius of the loop. This is because the centripetal force, which is responsible for keeping the bead in circular motion, is directly proportional to the square of the speed and inversely proportional to the radius of the loop.

What happens to the bead if the speed is too high or too low in the "Small bead - Circular loop Problem"?

If the speed of the bead is too high, the centripetal force may exceed the tension force from the string, causing the bead to break free from the loop. If the speed is too low, the bead may not have enough centripetal force to maintain circular motion and will fall off the loop.

How can the "Small bead - Circular loop Problem" be solved?

The "Small bead - Circular loop Problem" can be solved using Newton's laws of motion and the concept of centripetal force. By setting up and solving the equations of motion for the bead, the tension in the string and the speed of the bead can be calculated. This problem can also be solved using energy conservation principles.

Similar threads

Bead sliding on a Vertical Circular Loop versus in Free Fall
Replies
14
Views
2K
Which powers works on bead on a string?
Replies
2
Views
1K
Momentum and energy conservation in a vertical loop
Replies
13
Views
2K
What actually is the centripetal acceleration formula?
Replies
28
Views
2K
Flux induced in a circular loop
Replies
5
Views
1K
Circular loop of wire is concentric with a solenoid
Replies
10
Views
4K
A bead rests at the top of a fixed, frictionless hoop.
2
Replies
44
Views
8K
Time for Bead to Lose Contact: Solving for Friction and Tension Forces
Replies
12
Views
3K
Speed of a bead turned through X degrees
Replies
4
Views
2K
Faraday's law -- circular loop with a triangle
6
Replies
196
Views
20K

Hot Threads

Recent Insights

Back
Top