So, is my approach for finding angles efficient and accurate?

[Curiose]

For one of my current projects in computer vision (which really is a study in point clustering and tracking in a data stream of n-dimensional data), I have come up with a way to very quickly index a 2D angle between two points or the angle of a vector. Doing a little bit of investigation, and using +/- Infinity, I found a way to get an angle index through two divisions and one subtraction operation only using the position of the two points.

Here is the explanation and a Javascript implementation of the function
https://github.com/newsbubbles/mang

As some of you may know... finding the base angle of any two given points uses trig functions, and I have read people saying that it is impossible to find the angle. I threw radians and other such concepts out of the window as while they are very accurate, they take too long to process for hundreds of point samples at rates higher than 30 samples per second. Besides that, while having the exact angle is very useful for exact calculations, the idea of rotation-translation-size invariant memory (fuzzy memory?) is very important for object recognition or shape categorization in images or video.

This work may have already been done... but I am looking for some feedback and maybe some contributions to the idea. Also, if you know someone else who has already done this, please let me know.

Not sure if the image shows up on github properly, so here is the diagram which explains how I approached the problem...

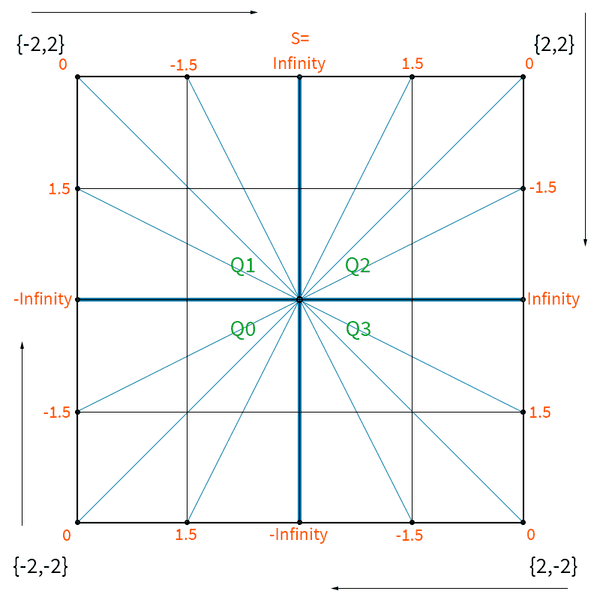
To put it briefly, by playing with the ratios between the points, I found a repeating pattern in each quadrant which I use to create a quadrant-specific angle index.

 

[jedishrfu]

An interesting algorithm, basically, you are replacing trig calculations with a lookup table, is that right?

This was a common scheme in early PC games with a small amount of memory and much slower processors than today.

This paper might be related to what you've developed independently for web applications.

http://www.lib.utexas.edu/etd/d/2004/arbaughj20424/arbaughj20424.pdf

and this wiki article on lookup tables:

https://en.wikipedia.org/wiki/Lookup_table

where there's a section on sin() lookup.

This game tutorial talks about getting angles and distances. Its not really relevant here but looked cool and could help some young gamer who reads this thread in the future:

https://www.raywenderlich.com/35866/trigonometry-for-game-programming-part-1

 

[Curiose]

Yes, thanks for your reply.

Using a lookup table, one in which the index pair is found by quadrant and angular slice limits

 

[DavidSnider]

I think this is known as https://en.wikipedia.org/wiki/Rational_trigonometry

 

[willem2]

Speed
Velocity of n=2 table approximation with an AMD 1.8Ghz quad-core

361 points in 4 milliseconds 90.25 angle calculations per millisecond or 90,250 angle approximations calculated per second

Isnt this really slow. The processor should be able to do more about 50 million ATAN instructions with 4 1.8 Ghz cores. ATAN is about 150 clockcycles.

 

[Curiose]

Actually, yes. but not really yes ;)

Anyway, here's the test I ran to get an actual benchmark on the same processor, but I forgot to mention I'm using latest version of firefox and running on windows... with no hardware acceleration on. So it's only CPU, and we're talking javascript running in a browser.

I ran a test with 100k iterations using two atan2 functions as shown below. Turns out that only took 637 milliseconds.

function getAngle(vector1, vector2){
    var angle = Math.atan2(vector2.y, vector2.x) - Math.atan2(vector1.y, vector1.x);
    if (angle < 0) angle += 2 * Math.PI;
    return angle;
}
var vecs = [{x:20,y:-3},{x:6,y:40},{x:-90,y:-30}];
var s = Date.now();
for (var i=0;i<100000;i++){
    getAngle({x:0,y:0},vecs[i % 3]);
}
var e = Date.now() - s;
console.log(e);

So you are correct, but the loss factor of time is maybe not comparable to "really".

90,250 in 1000 ms vs. 100,000 in 637 ms is a 35 - 40% loss in time, which is significant, but not an entire order slower.

@jedishrfu Doing further reading I realized that CORDIC was built into microprocessors decades ago :D

I guess the main difference also between the benchmark and my specific implementation of the angular lookup index is that: while having the exact angle is preferable in cases where exact calculations must be made, mAng performs an angle approximation within some angle of radial resolution, whereas the function I made for the benchmark does a precise angular calculation. Since I am using this to make an angular histogram for generating radial invariant memory plus allow for scaling and slight shape transformations of the features I would need to actually change the benchmark to include returning a 2D lookup index. This means I would still have to use calculation to downsample the angles. I'd need at least one division calculation, one quadrant logic block and one Math.floor, also taking up some extra clock cycles after each angle calculation with the two atan2 functions.

I guess really your answer is... What I made is a specialized function for a specific task. The built in atan functions are for precise angular calculation, which is not necessarily the end product that needs to come out of a function which uses an index to store a count of edges that fall within the same n-resolution angular slices when traced. Using the atan2 functions generates a precise number who's preciseness must be decimated in order to find the right index, which seems to be extra steps for the purposes of the function.

If you add in the missing functionality for returning the 2D index to the benchmark test, maybe the 35% - 40% loss turns into no loss. I'm tempted to do it just to see, but must start the rest of my day :D