- #1
chetzread
- 801
- 1
Homework Statement
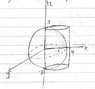
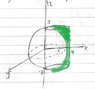
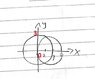
By using cylindrical coordinates , evaluate the volume of solid bounded on top of sphere (x^2) + (y^2) + (z^2) = 9 and it's sides by (x^2) + (y^2) = 4x . [/B]
Homework Equations
The Attempt at a Solution
I have sketched out the diagram , but i dun know which part is the solid formed... Can someone highlight the solid formed ? [/B]