Solve my Mechanical Motion Puzzle: 18in(7lbs)

[around86]

Homework Statement

I am trying to figure out the formula to help me build something

Relevant Equations

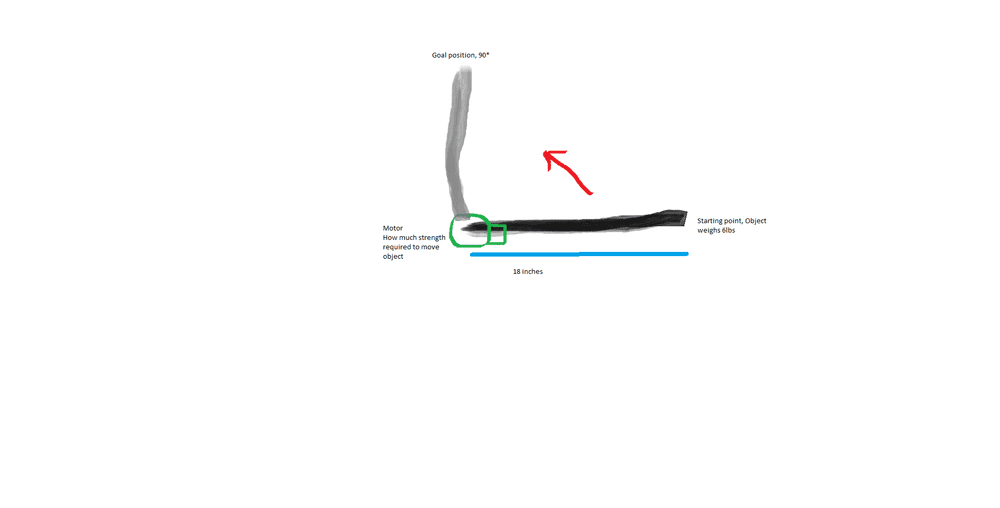
I want to know how to solve: What is the power or torque required to lift an 18 inch long object, that is 6-8 pounds, from an anchored end.

I am at my wits end with trying to find this formula. So far all I've gotten is I need to figure out mechanical power, maybe torque? I can't figure out the formula for this motion as it is like negative leverage. I want to build a machine that can do this thousands of times so I also need to figure the longevity of the motor's power required. My degree is in hospitality management, and the only math or physics classes I could really push my limits in is finance. I am trying to learn, and am starting to hit a wall. If anyone has any idea where I can look to find this information I would greatly appreciate it. 18 inches(7lbs) from flat position to 90 degrees vertical, and back down softly.

***my previous post on this was my hasty attempt at solving my headache without reading the forum rules and I apologize for breaching. Thank you

 

[haruspex]

In its initial position, the arm exerts a torque about the axis. Can you calculate that? That is the torque your motor needs to exceed in order to lift the arm. Once it starts to rise the required torque will decrease, so the arm will accelerate. You may need some way to ease off the motor to avoid coming to a violent stop at the top.

The longevity of the system will depend on what wears out and why. You will need the motor's specs.

 

[around86]

Thanks @haruspex! I have been trying to find the formula to calculate reqd torque with the length of the object causing greater resistance at first. I believe I will be able to program torque speed by rotation, but I am not sure how to get the first part

 

[haruspex]

Thanks @haruspex! I have been trying to find the formula to calculate reqd torque with the length of the object causing greater resistance at first. I believe I will be able to program torque speed by rotation, but I am not sure how to get the first part

Draw a force diagram for the arm. Where does its weight act? How far is that from the axis? So what is the torque the weight exerts about the axis?

 

[Lnewqban]

Homework Statement:: I am trying to figure out the formula to help me build something

The worst condition is the horizontal position, as explained above.
That torque equals the weight times half the length of the door.
Applying a motor torque directly to the axis of rotation creates the problem of a robust key or other type of shaft-door joint.

Normally, another type of linkage located away from the axis allows for a lighter mechanism.
For that reason, it is important to carefully think about the options that actual conditions allow to your problem.

 

[Tom.G]

Welcome to PF @around86 !

I'm going to assume that your post is accurate and this is not Homework. That said, I'm going to break the Homework rules a bit and try to answer your question.

You may have run across the term "Center of Mass" (CM), also called "Center-of-Gravity" (COG). That is the point in an object where its Mass (or weight) can assumed to be concentrated so that calculations are easier. If that horizontal thing you want to rotate has uniform weight along its length, then the CM is in the center. For your 18" object, that puts the CM at 9" from the pivot.

So for an 8 pound mass at 9" from the pivot, the torque needed to support it would be 8 x 9 = 72lb.in. Note that this is the torque to support it; if you want to get it moving you will need a little bit more torque to overcome the inertia.

Now to address the torque variation over the rotation angle:
Obviously the torque will be maximum at the horizontal position. Just multiply that 72in.lb by Cos(α), where α is the angle from horizontal. For instance at 30° elevation Cos(30) = 0.866. So multiply 72 x 0.866 = 62.4lb.in.

Additional torque is needed to get it moving, or to slow it down at the top of travel. How much additional depends on what acceleration is desired, i.e. how quickly you what it to reach a given speed. That I'll leave to others here who know that stuff by heart, I would have to look it it up, somewhere!

edit: added "COG" definition

Have Fun!

Cheers,
Tom

p.s. you've got me curious. can you tells us the application without giving away any secrets?