Solve Situational Problems Involving Trigonometric Identities

[ukumure]

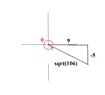
Hi! I am so confused about the given and what is being asked, I don't know how to solve it. This topic is solving situational problems involving trigonometric identities. Your help would be a big one for me :) Thank you so much in advance!

 

[Greg]

First, we need to establish $\sin\theta$ and $\cos\theta$.
$9^2+(-5)^2=106$ (Pythagorean theorem)
so $\sin\theta$ is $\sqrt{\frac{|-5|}{106}}, \text{that is}, \left(\frac{opp}{hyp}\right)$ and $\cos\theta$ is $\frac{3}{\sqrt{106}}, \text{that is}, \left(\frac{adj}{hyp}\right)$ (recall that $\sin\theta$ is the magnitude of the opposite side of the right-angled triangle containing $\theta$ divided by the hypotenuse)

Hence $\sin\theta+\cos\theta=\frac{3+\sqrt{|-5|}}{\sqrt{106}}$.

 

[ukumure]

First, we need to establish $\sin\theta$ and $\cos\theta$.
$9^2+(-5)^2=106$ (Pythagorean theorem)
so $\sin\theta$ is $\sqrt{\frac{|-5|}{106}}, \text{that is}, \left(\frac{opp}{hyp}\right)$ and $\cos\theta$ is $\frac{3}{\sqrt{106}}, \text{that is}, \left(\frac{adj}{hyp}\right)$ (recall that $\sin\theta$ is the magnitude of the opposite side of the right-angled triangle containing $\theta$ divided by the hypotenuse)

Hence $\sin\theta+\cos\theta=\frac{3+\sqrt{|-5|}}{\sqrt{106}}$.

THANK YOU SO MUCH! )

 

[skeeter]

$\cos{\theta} = \dfrac{x}{r} = \dfrac{9}{\sqrt{106}}$

$\sin{\theta} = \dfrac{y}{r} = \dfrac{-5}{\sqrt{106}}$

$\cos{\theta} + \sin{\theta} = \dfrac{4}{\sqrt{106}}$