Solving a Rod-Particle System: Troubles with Forces

[greg_rack]

Homework Statement

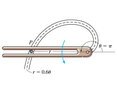
Using a forked rod, a smooth cylinder P, having a mass $m$, is forced to move along the vertical slotted parth $r=(0.6\theta)m$, with $\theta$ in radians. If the cylinder has a constant speed $v_c=2m/s$, determine the force of the slot on the cylinder at the instant $\theta=\pi rad$.
Assume the cylinder is in contact with only one edge of the rod and slot at any instant.

Relevant Equations

velocity and acceleration components in polar coordinates, Newton's 2nd law.

Hello guys,

here's another problem I'm having troubles with(I have attached my working out not for laziness, but clarity since steps are many).
I started by defining a polar coordinate system, and then drawing the FBD and KD to get to the equations of motion for particle P.
I identified 3 acting forces: a normal force, a force($F_r$) exerted by the rod in the transverse direction such as(at this instant) the weight.
I calculated $\psi$ so to be able to decompose $N$ in its polar components, and wrote the EOM wrt my drawing.
After a whole bunch of tedious chain rule I managed to calculate first and second derivatives of $r, \ \theta$ in order to compute the accelerations for inertial forces.

Solving now the EOM for N and $F_r$, I end up with the correct value for N, but the wrong one for $F_r$, which should(curiously?) apparently be equal to the weight of the cylinder($mg=3.92N$), as opposed to my result($-mg+Ncos\psi +ma_{\theta}=-3.384N$).

What have I done wrong?

 

[Lnewqban]

Could you post a diagram of the relative positions and directions of movements of the rod, the slot and the cylinder?
I can’t clearly see the situation from your work, sorry.

 

[greg_rack]

Could you post a diagram of the relative positions and directions of movements of the rod, the slot and the cylinder?
I can’t clearly see the situation from your work, sorry.

Sure!

 

[ergospherical]

I wonder if we should cross-check results, given that it's a little bit fiddly. I denoted $\alpha \equiv 0.6 \ \mathrm{m}$, so that the curve is given by $r(\theta) = \alpha \theta$. Then for the first derivatives,\begin{align*}
\dot{\theta} = \dfrac{v_c}{\alpha\sqrt{1+\theta^2}}, \quad \quad \dot{r} = \dfrac{v_c}{\sqrt{1+\theta^2}}

\end{align*}Whilst for the second derivatives,\begin{align*}
\ddot{\theta} = \dfrac{-v_c^2 \theta}{\alpha^2(1+\theta^2)^2}, \quad \quad \ddot{r} = \dfrac{-v_c^2 \theta}{\alpha(1+\theta^2)^2}
\end{align*}If $\mathbf{F}$ is the net force, the equations of motion should look like (as you wrote),
\begin{align*}
\dfrac{1}{m} \underbrace{\mathbf{e}_r \cdot \mathbf{F}}_{\mathrm{radial \ force}}&= \ddot{r} - r\dot{\theta}^2 = \dfrac{-v_c^2 \theta(2+\theta^2)}{\alpha(1+\theta^2)^2} \\

\dfrac{1}{m} \underbrace{\mathbf{e}_{\theta} \cdot \mathbf{F}}_{\mathrm{tangential \ force}}&= 2\dot{r} \dot{\theta} + r\ddot{\theta} = \dfrac{v_c^2(2+\theta^2)}{\alpha(1+\theta^2)^2} = -\dfrac{1}{\theta} \left( \dfrac{1}{m} \underbrace{\mathbf{e}_r \cdot \mathbf{F}}_{\mathrm{radial \ force}} \right)
\end{align*}which implies that $\mathbf{e}_{r} \cdot \mathbf{F} = -\theta \mathbf{e}_{\theta} \cdot \mathbf{F}$. For the forces I have that
\begin{align*}
\mathbf{e}_r \cdot \mathbf{F} &= N \sin{\psi} \\
\mathbf{e}_{\theta} \cdot \mathbf{F} &= -N \cos{\psi} + F_{\mathrm{rod}} + mg
\end{align*}Is that consistent with your results so far, after plugging in $\alpha$? If so, then one may proceed to evaluate all of the $\theta$-dependent quantities at $\theta = \pi$. In that case the angle $\psi$ satisfies $\tan{\psi} = \pi$, I believe, and given $m = 0.4 \ \mathrm{kg}$ you can solve for $N$ and $F_{\mathrm{rod}}$. (The size of $F_{\mathrm{rod}}$ does indeed appear to come out as $|F_{\mathrm{rod}}| = mg = 3.92 \ \mathrm{Newtons}$).

 

[greg_rack]

Thank you so much @ergospherical for the effort you put in replicating all the calculations, that's brilliant!
Our results for time derivatives matched, and so did the whole procedure... the only thing I did differently was defining the radial axis pointing inwards and not outwards as you did, but apparently it was sufficient to mess the whole result up! Does it make sense? What should have I done in order to make calculations coherent with the coord. system defined as such?

Filling values in your equation give: $N=-0.88N, F_r=-3.92N$, which are indeed correct!
But, for clarity, do the minus signs only indicate that you guessed the wrong directions for N and $F_r$(pointing outwards and to the bottom respectively), and that thus they act in the reversed ones?

 

[ergospherical]

the only thing I did differently was defining the radial axis pointing inwards and not outwards as you did, but apparently it was sufficient to mess the whole result up! Does it make sense? What should have I done in order to make calculations coherent with the coord. system defined as such?

The results for the acceleration components in polar coordinates are based on having the $\mathbf{e}_r$ basis vector pointing away from the origin and the $\mathbf{e}_{\theta}$ basis vector pointing in the direction of increasing $\theta$.

You could of course write down the equations in a slightly different coordinate system, like the one you're suggesting with $\mathbf{e}_r' = - \mathbf{e}_r$, but then $a_r' = -a_r =-(\ddot{r} - r\dot{\theta}^2)$. Seems like more trouble than it's worth... best to stick with conventions.

But, for clarity, do the minus signs only indicate that you guessed the wrong directions for N and $F_r$(pointing outwards and to the bottom respectively), and that thus they act in the reversed ones?

I believe so, yes. I'll admit I didn't expect the forces to point the other way around; I don't know if I can think of an intuitive way to explain it. Maybe somebody else can, assuming it's right!

 

[greg_rack]

You could of course write down the equations in a slightly different coordinate system, like the one you're suggesting with $\mathbf{e}_r' = - \mathbf{e}_r$, but then $a_r' = -a_r =-(\ddot{r} - r\dot{\theta}^2)$. Seems like more trouble than it's worth... best to stick with conventions.

Great, you're right!

I believe so, yes. I'll admit I didn't expect the forces to point the other way around; I don't know if I can think of an intuitive way to explain it. Maybe somebody else can, assuming it's right!

Yes, indeed! Especially the force exerted by the rod acting upwards gets me quite confused; the only thing I can think about is that this might be caused by the vertical path, thus with weight as well acting on P.
What a cool exercise, and I also found curious the fact that $\vec{F_r}=-\vec{W}$, or at least unexpected... wasn't it?

 

[ergospherical]

There is also the nice property of the Archimedian spiral that, at constant speed, the radial acceleration is nothing but the tangential acceleration scaled by the factor of $-\theta$.

Thinking about it, I think I do have a decent explanation as for the signs. In a Frenet-Serret basis, the component of acceleration in the direction of the tangent vector $\hat{\mathbf{t}}$ to the curve is nothing but the derivative of the speed along the curve, which is zero: $a_t = m \dfrac{dv_c}{dt} = 0$. Therefore the component of the net force in the direction of $\hat{\mathbf{t}}$ is zero. Since, at $\theta = \pi$, the weight has a positive component of force in the direction parallel to the tangent vector $\hat{\mathbf{t}}$, and $\mathbf{N}$ has no component of force in the direction parallel to $\hat{\mathbf{t}}$, it follows that $\mathbf{F}_{\mathrm{rod}}$ must have a negative component of force in the direction parallel to $\hat{\mathbf{t}}$ (equal in magnitude to the component of weight, for equilibrium). Therefore $\mathbf{F}_{\mathrm{rod}}$ must point upward, not downward.

In fact, it's probably easier to do the problem in Frenet-Serret coordinates!