Solving Banked Curve Problem: Max Velocity

[dl447342]

Homework Statement

A car is driving in a circle of radius R around a banked curve that makes an angle of $\theta$ with the horizontal. If the coefficient of static friction between the cars tires and the road is $\mu_s$, then what is the maximum speed the car can travel so that it does not slide?

Relevant Equations

$f_s^{\max} = \mu_s n, \sum \vec{F} = m \vec{a}, a = mv^2/R.$

Here's a FBD I made for this question.

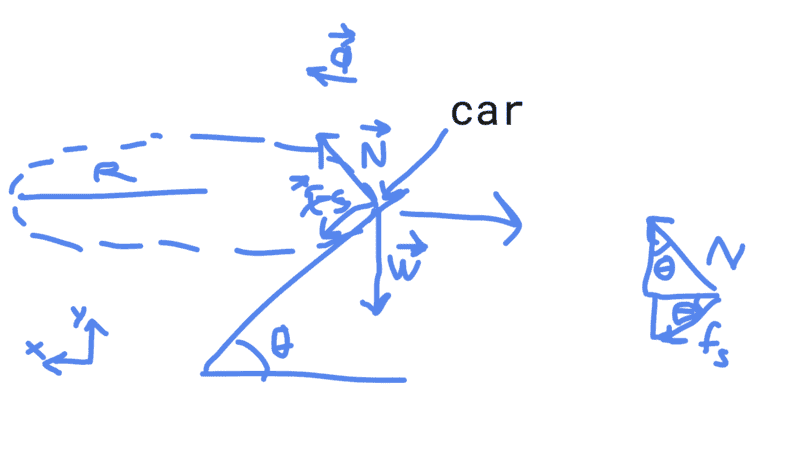
From the diagram, I obtained that $-W + N \cos\theta - f_s \sin\theta = 0$. And $N\sin\theta + f_s \cos\theta = ma = \frac{mv^2}{R} \leq N\sin\theta + f_s^{\max} \cos\theta = \frac{mv_{\max}^2}{ R}$. Solving these equations, and using the angle addition formula for tan, I get $v_{\max} = \sqrt{gR \tan (\theta + \theta_s)}$. If $\theta_s$ satisfies $\mu_s = \tan \theta_s$ and $\theta > 90^{\circ} - \theta_s,$ then $tan (\theta + \theta_s) < 0,$ so maybe $v_{\max} = \infty$? And if so, why? Is it because in that case $f_s(1-\mu_s \tan\theta) \leq \mu_s W$ is always true so that $f_s^{\max} = \infty$? Btw, I got the latter inequality by using the fact that $f_s^{\max} = \mu_s N$ and the very first equation; the first equation gives $f_s = \frac{N\cos\theta - W}{\sin\theta}$ and this is at most $\mu_s N =\frac{ \mu_s (W + f_s\sin\theta)}{\cos\theta} \Rightarrow f_s (1-\mu_s \tan\theta) \leq \mu_s \frac{W}{\cos\theta}$.

 

[kuruman]

If $\theta +\theta_s >90^{\circ}$, then you have a negative number under the radical. When that happens, it means that you have an unphysical situation, i.e. what is desired to happen, in this case the car not slipping, cannot happen.

 

[Lnewqban]

Consider that the car can slide up and out of the curve or down and inside the curve.
As the angle of the bank increases from horizontal, the maximum non-sliding speed with which the car can travel also increases.
That happens because the component of the car's weight that is parallel to the surface of the banked road helps the lateral friction force to prevent a slide out.

 

[haruspex]

That happens because the component of the car's weight that is parallel to the surface of the banked road helps the lateral friction force to prevent a slide out.

Plus, the component of the centrifugal force normal to the road increases, increasing the maximum frictional force for the same speed.

 

[haruspex]

in this case the car not slipping, cannot happen

The assumption made is that the car might be on the point of slipping, so that is what must be impossible.

 

[kuruman]

The assumption made is that the car might be on the point of slipping, so that is what must be impossible.

Yes, I should have been more careful with my use of language. I do not wish to restart the conversation of whether a mass "on the verge of slipping" is slipping or not.

 

[bob012345]

Edit: Note that the following is not a solution to the homework problem and it not necessary to solve the homework problem.It is interesting to think about the direction of the static friction which depends on the velocity. Obviously if the car is parked on the banked road the friction points up the incline. If the car is going fast it can point down the incline. It seems there is a velocity for each angle at which there is no friction. By assuming no friction we get the relationship $v = \sqrt{gR Tan(\theta)}$ which I plotted below as $\frac{V}{\sqrt{gR}}$. For a given angle if the speed is faster than the curve the friction points down which is red area and if less it points up which is the green area. The point is for $\theta=\large\frac{\pi}{4}$ and $v = \sqrt{gR}$. The red and green area's only tell the direction of the friction not velocity vs. angle. Note that at exactly $\large\frac{\pi}{2}$ the friction would have to point up. I think this is correct but if there are any flaws in my logic please point them out. Thanks.

 

[bob012345]

Looking at the OP, the correct solution is there $v_{max} = \sqrt{gR ~tan( \theta + \theta_s)}$ with $\theta_s = arctan(\mu_s)$. But $v_{max}$ depends on the bank angle of the road and the coefficient of friction. I got a slightly more complicated but equivalent answer;

$$v_{max} = \sqrt{gR \left(\frac{sin(\theta) + \mu_s cos(\theta)}{cos(\theta) - \mu_s sin(\theta)}\right)}$$

So if for a given $\theta$ and $\mu_s$, $cos(\theta)=\mu_s sin(\theta)$, then $v_{max} =∞$ but in general there is a family of curves for different friction coefficients.

I added a region for $\mu_s = 1$ as an example. For $\mu_s=0$ it is the original curve. All friction coefficient curves are between these. Any point in the orange region will slip. The actual curve is the same as the zero friction curve but translated left a bit. The line is the angle in which a car can go any speed without slipping for that coefficient of friction. Note that for $\mu_s=1$ that is $\large\frac{\pi}{4}$. Less friction means a steeper bank angle to go at any speed without slipping.

 

[kuruman]

Nice work. To complete the graph, you might wish to consider a fourth color to separate the green region. If the car goes too slow, it will slide down the incline. It should be easy to do because the free body diagram remains the same except the friction reverses direction. All you have to do is reverse the sign of $\mu_s$ in the formula you already have and replot.

 

[haruspex]

Yes, I should have been more careful with my use of language. I do not wish to restart the conversation of whether a mass "on the verge of slipping" is slipping or not.

To be clear, it wasn't just a nitpick. In the unphysical case, it is the car slipping that cannot happen, not the car not slipping.

 

[bob012345]

I added the low speed slip region in blue at @kuruman's suggestion;

For maximum friction coefficient $\mu_s=1$ Orange is the high speed slip region.

For $\mu_s=0.5$

 

[kuruman]

To be clear, it wasn't just a nitpick. In the unphysical case, it is the car slipping that cannot happen, not the car not slipping.

Yes, I am with you. I put a not where a not did not belong in #2.

 

[haruspex]

Yes, I am with you. I put a not where a not did not belong in #2.

It's easy to get tied in nots.