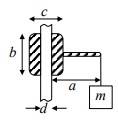
When the problem says that there is a "nut" on the vertical rod, it seems that it is really talking about a "sleeve", "bushing" or "pair of plates on either side of the rod". This assembly is not tightly clamped onto the rod. Instead, it is free to slide up and down. However, it is machined or clamped to a tight tolerance so that it fits snugly and is not free to tilt or wobble as it slides. It presents zero frictional resistance unless a torque is present.
A "nut" would indicate the presence of threads. A "nut" would not be free to slide up and down on a threaded bolt.
We may begin by assuming that the assembly is in static equilibrium, just on the verge of slipping. Further, I would suggest assuming that the assembly itself has negligible mass -- gravity only acts on the attached mass m.
You say that you have produced a free body diagram. May we see that diagram? Or can you at least list the moments that you have identified on that diagram and give us any equations that you have formed from them?
As it stands, you have showed no work -- only asserted that you have made some effort.
Edit: There is an additional assumption that may turn out to be necessary. Without it, the situation appears to be statically indeterminate: "Both contact patches are on the verge of slipping"