Solving initial value problem using Laplace transform

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this problem,

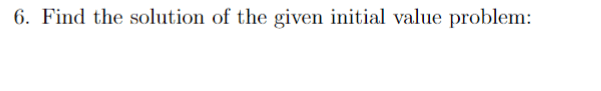
I'm confused how,

However, not sure how to go from here.
$$
f(t) = \begin{cases}
1 & \text{if } 0 \leq t < 10\\
0 & \text{if } t \geq 10

\end{cases}
$$
By definition Heavside function is,
$$
H(t - 10) = \begin{cases}
1 & \text{if } t < 10\\
0 & \text{if } t \geq 10


\end{cases}




1 - H(t - 10) = 1 - \begin{cases}
1 & \text{if } t < 10\\
0 & \text{if } t \geq 10


\end{cases}
$$
However, I don't know where to go from here. Does anybody please know?

Thanks for any help!

 

[anuttarasammyak]

Heaviside function is easily Laplace transformed. See https://math.libretexts.org/Bookshe...orm/5.03:_Heaviside_and_Dirac_Delta_Functions