Zeeshan Ahmad
Gold Member
- 24
- 9
Thread moved from the technical forums, and the OP has been reminded to show their work.
- Homework Statement
- Obtain eq 20(show in the below picture)
Directly from the waves equation by separation of variable
- Relevant Equations
- linear combinations of sinusoidal waves
While I was doing a problems of chapter 9 of DJ griffith electrodynamics
I came across this problem 4
Problem statement
Obtain eq 20(show in the below picture)
Directly from the waves equation by separation of variable
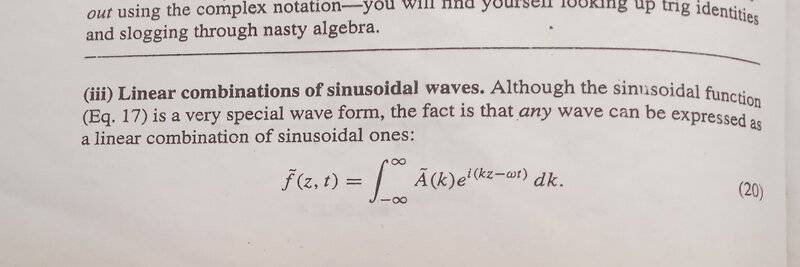
Could I have a straight solution in your word
Thank you
I came across this problem 4
Problem statement
Obtain eq 20(show in the below picture)
Directly from the waves equation by separation of variable
Could I have a straight solution in your word
Thank you