I Solving this system of equations in different ways

[help]

TL;DR Summary

system of equations, circumference and parable

Good night!
How do I find the values of a (real) so that the solution of this system is?

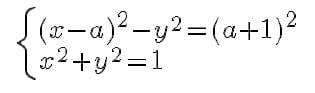
(i) just an ordered pair?
(ii) exactly two pairs.
(iii) exactly 3?
(iv) is there a place where you have more than 3 pairs as an answer?So...
I thought like this: I developed the first part. I solved the system and found x²-ax-a-1 = 0

(i) I made the delta zero by finding a = -2. Point (-1.0)
(ii) I thought about doing a = 0 getting x = + - 1 finding the points (-1,0) and (1,0).

item iii. Making the drawing it is possible to verify -1<a<0 that but I don't know why.

I also know that there is no way but I don't know how to prove it.

 

[mfb]

For (i) there are more solutions. Consider what happens e.g. for a=2. Yes, $x^2 - 2x - 3 = 0$ has more than one solution - but does that lead to more than one intersection of the curves?

(ii) looks good.

(iii) did you draw a sketch? You have a circle and a hyperbola with two sides. Clearly (-1,0) is always a solution, to get three solutions you need the other part of the hyperbola intersect the circle in two more points. What does that mean for the position of the hyperbola where y=0? There are also more solutions here that you didn't find.

Ultimately all real values of "a" should be in one of the answers. If your ranges together don't cover all real values then you missed something.

 

[help]

hello, thanks for answering

i) a≤ -1 or a>0 * a=-1asymptote

ii) a=0

iii)-1<a<0

iv) does not existI can see it by looking at the graph, but how can I prove it algebraically?

 

[mfb]

a=-1 has more than one solution. So does the range between -1 and -2.

Looking at the graph tells you which kind of solution to look for and which ranges to look at, you can then study these algebraically.

 

[help]

ok
i) a≤ -2 or a>0
when we calculate delta = 0, find a = -2 as the tangency point. But I saw through the graph that the system will have only one ordered pair as a solution for <= - 2 or a> 0

ii) a=0

iii)-2<a<0

iv) does not exist

solving the system we find x²-ax-a-1=0

∆ = (-a)² - 4.1.(- a - 1) = a² + 4.a + 4 = (a + 2)² --->

√∆ = |a + 2 |

How to interpret?

We find roots
-1 and a+1 to a>-2 e

a+1 and -1 to a<-2

how to write?

to a>-2

a=0 2-point intersection

a>0 1-point intersection

-2<a<0 3-point intersection
and to a<-2

1-point intersection

 

[mfb]

Looks good.