- #1
jaumzaum
- 434
- 33
I was studying the twin paradox (of Einstein special relativity) and everything was working well until I get to the traveler's spacetime diagram.
First let me introduce the paradox for you to understand the diagram.
Pam is the twin sister of Joe. Pam goes out Earth in 2007 in a spaceship with v = 0.6c (velocity that Jim measures) for a 3 light-years round trip (again, distance that Jim measures). Every year that passes in Pam calendar, she sends a message to Jim ( the message travels with light-speed). So do Jim. At the end, they find out Pam is 2 years younger than Jim.
The spacetime diagram in the Jim's frame of reference is:
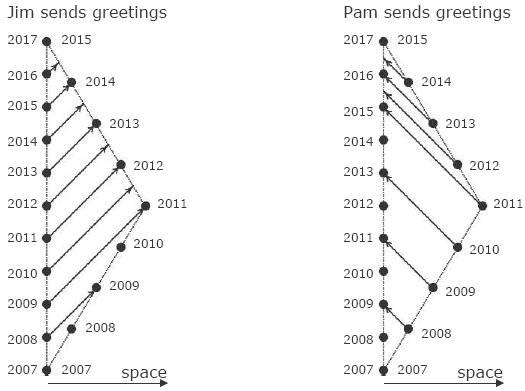
But when we try to put this in the Pam's frame of reference it goes like this:
Or, if we draw the message lines too (red lines)
http://img109.imageshack.us/img109/643/33306470.png
I'm confused about the following:
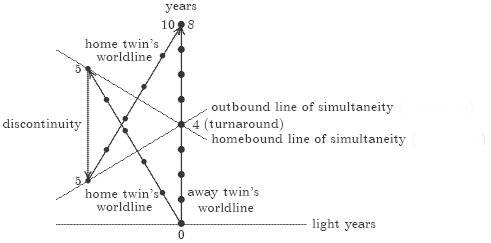
1) What is this discontinuity in the diagram? What does it means?
2) In 2009 (Pam's calendar) Pam sends a New Year message to his brother, and we can see the message intersects the diagram 2 times (in 2011 and 2014, Jim's calendar ). What does it mean? Will Jim receives 2 times the same message sent by Pam?
3) In the discontinuity line, 2 messages sent by Pam arrives. What does it mean? Seen that the turnaround occurs in a very short period of time, will Pam receive this 2 messages at the turnaround, and simultaneously?
First let me introduce the paradox for you to understand the diagram.
Pam is the twin sister of Joe. Pam goes out Earth in 2007 in a spaceship with v = 0.6c (velocity that Jim measures) for a 3 light-years round trip (again, distance that Jim measures). Every year that passes in Pam calendar, she sends a message to Jim ( the message travels with light-speed). So do Jim. At the end, they find out Pam is 2 years younger than Jim.
The spacetime diagram in the Jim's frame of reference is:
But when we try to put this in the Pam's frame of reference it goes like this:
Or, if we draw the message lines too (red lines)
http://img109.imageshack.us/img109/643/33306470.png
I'm confused about the following:
1) What is this discontinuity in the diagram? What does it means?
2) In 2009 (Pam's calendar) Pam sends a New Year message to his brother, and we can see the message intersects the diagram 2 times (in 2011 and 2014, Jim's calendar ). What does it mean? Will Jim receives 2 times the same message sent by Pam?
3) In the discontinuity line, 2 messages sent by Pam arrives. What does it mean? Seen that the turnaround occurs in a very short period of time, will Pam receive this 2 messages at the turnaround, and simultaneously?
Last edited by a moderator:


