Specific Speed of Hydro-turbines

[I_am_learning]

I am again confused at this. As far as I know, specific speed of a turbine of given Shape and Size is defined as -"The speed at which geometrically similar (i.e. scaled down Version) turbine would rotate when provided with unit head and unit discharge"
The general text-book derivation for specific speed gives

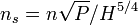
But, I guess its written the other-way-round. I mean, most of the time, we have our turbine, and we have the specific speed for our turbine (owing to its shape & provided by the manufacturer), and we would like to find out at what speed it would rotate when we provide some head H and Discharge Q (P). So, I think, the useful way of writing the formula would be
N = Ns * H^(5/4) / sqrt(P) .
That is all for my understanding.
Now my confusion. :)
I also find that text-books gives charts for Ns Vs Head ? I thought, specific speed is dependent only on Turbine Geometry. Then how come, say a franchise turbine of given geometry have different specific speed for different heads? I feel like It kills the very own definition of specific speed.
Thanks for reading.

 

[Navin A S]

I think your confusion arises due to a misunderstanding of the concept of specific speed. Specific speed is not a static value, it is dependent on the head and discharge of the turbine. So, when you provide a turbine with different heads and discharges, the specific speed will vary accordingly. The charts that you find in textbooks are actually plots of the specific speed for various heads and discharges. So, when you look at them, you can find the specific speed for a particular turbine based on the head and discharge you are providing it with. Hope this helps!