stunner5000pt
- 1,447
- 5
- Homework Statement
- Consider the diagram given. All surfaces have friction (u(s) & u(k)). When the system is released from rest, the mass M is heavy enough to pull m1 and m2 up the slope. m2 remains at rest with respect to m1. Determine the acceleration of the system in terms of the given variables
M, m1, m2, u(k) and u(s)
- Relevant Equations
- Newton's 2nd law
Friction = coefficient of friction x normal force
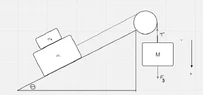
I've posted my attempt at a solution but I haven't gone through the whole process of putting together equations 1 -4 yet as I wanted to clarify if I'm on the right path
My doubt lies in the formulation of equation 4 - the force equation for the stacked block. Since we don't know the acceleration of the masses and we don't know if mass M is heavy enough to cause m2 to slide, do we leave F_{12x} undetermined and not equate this to \mu_{s} F_{N} ?
Are all the equations considering all variables or did I miss anything in my formulation so far? I'm happy to retype all that is written on the solution attempt in tex if the writing is illegible - let me know!
Appreciate all your input in advance & thank you :)
