Static Equilibrium Pulley and free body diagram

In summary, the conversation discusses a problem in which a system is in equilibrium and equations are used to solve for tension and theta. The equations are set to zero and rearranged to find the values. The conversation also mentions the importance of using pictures to help solve the problem.
  • #1
sharp12
4
0

Homework Statement


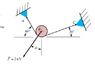
Attached is the picture of the problem and my free body diagram.
The system is in equilibrium.

Homework Equations



Fy = 0 Fx = 0

The Attempt at a Solution



I'm having trouble solving the two equations that I arrive with...

I use +x to the right, and +y up.

For the forces in x: -TacCos(60) + TacCos(20) - 2000Sin(theta) = 0

For the forces in y: TacSin(60) + TacSin(20) - 2000Cos(theta) = 0

When trying to solve these two equations, I tried adding them together and setting them equal to each other but I've had no luck. What am I doing wrong or missing here?
 

Attachments

  • Capture.PNG
    Capture.PNG
    5.4 KB · Views: 940
  • Capture2.PNG
    Capture2.PNG
    1.5 KB · Views: 739
Physics news on Phys.org
  • #2
Hi sharp,

I guess you need to find theta and the tension so as the pulley is n equilibrium.

Your equations look correct. Move the term with theta on the other side, then divide the equations: the tension will cancel and you can solve for theta.

ehild
 
  • #3
ehild said:
Hi sharp,

I guess you need to find theta and the tension so as the pulley is n equilibrium.

Your equations look correct. Move the term with theta on the other side, then divide the equations: the tension will cancel and you can solve for theta.

ehild


Hi ehild,

Thank you! That worked out quite nicely. :)!
 
  • #4
You are welcome. :smile: I was really pleased with your suggestive pictures. Remember the method. ehild
 
  • #5


I would first commend you on correctly setting up the free body diagram and using the correct equilibrium equations. It seems that you are on the right track in terms of solving the equations, but you may be missing a key component in the problem.

In order to fully solve the equations, you need to know the values of the tensions in the two ropes, Tac and Tbc. These tensions can be calculated using trigonometric relationships and the given angles and forces. Once you have these values, you can substitute them into your equations and solve for the unknown variable, theta.

Additionally, it may be helpful to draw a separate free body diagram for each pulley in the system, as this can help you visualize the forces acting on each object and make it easier to solve the equations.

Overall, it seems like you have a good understanding of the concepts involved in this problem. Keep working at it and don't hesitate to ask for help if you get stuck. Good luck!
 

FAQ: Static Equilibrium Pulley and free body diagram

What is static equilibrium in the context of a pulley and free body diagram?

Static equilibrium refers to a state in which an object is at rest and all forces acting on it are balanced. In the context of a pulley and free body diagram, this means that the forces acting on the pulley and the objects attached to it are equal and opposite, resulting in a stable and balanced system.

How do I draw a free body diagram for a pulley system?

To draw a free body diagram for a pulley system, start by identifying all the objects and forces involved. This includes the pulley, the objects attached to it, and any external forces such as gravity or tension. Then, draw a simplified diagram of the pulley and the objects, representing them as point masses. Finally, label all the forces acting on each object with arrows indicating their direction and label each force with its appropriate magnitude.

What is the purpose of using a free body diagram in analyzing a pulley system?

A free body diagram is a visual representation of the forces acting on an object, and it is a useful tool for analyzing the forces in a pulley system. By drawing a free body diagram, you can easily identify the forces acting on each object and determine whether the system is in static equilibrium or whether any forces need to be adjusted to achieve equilibrium.

Can a pulley system be in static equilibrium if there is friction present?

Yes, a pulley system can still be in static equilibrium even if there is friction present. In this case, the forces acting on the pulley and the objects attached to it will need to be adjusted to account for the friction force. The friction force will act in the opposite direction of the motion of the object and should be included in the free body diagram.

What factors can affect the static equilibrium of a pulley system?

Several factors can affect the static equilibrium of a pulley system, including the weight and mass of the objects attached to the pulley, the angle at which the pulley is positioned, the presence of friction, and the magnitude and direction of external forces such as gravity. Any changes in these factors can impact the equilibrium of the system and may require adjustments to be made to the forces acting on the objects.

Similar threads

Is it friction or tension acting on the person hanging on a rope?
Replies
4
Views
475
Block on top of an inclined plane, with a rough surface, that moves with constant acceleration
2
Replies
41
Views
2K
Which block reaches the wall faster?
Replies
2
Views
600
Pulleys with Torque: Free Body Diagram Analysis
Replies
34
Views
3K
Statics problem (moment and equilibrium)
Replies
6
Views
2K
Statics free body diagram (frames and machines)
Replies
5
Views
3K
How to find the equilibrium position of three masses (two of them fixed)?
Replies
4
Views
1K
Solving Free-Body Diagrams for Moving Nuts on Rods: Tips and Techniques
Replies
9
Views
1K
Free Body Diagram of Mass-Spring System
Replies
5
Views
540
Free body diagram for an inverted pendulum in the rolling sphere
Replies
9
Views
2K

Hot Threads

Recent Insights

Back
Top