- #1
belleamie
- 24
- 0
HI there, I was assigned 7 homework problems but there were three I didnt know how to answer...
please help, any hints on how to start would be appreciated.
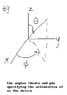
#3 the state of spin-1/2 particle that is spin up along the axis whose direction is specified by the unit vector n=sin (theta) cos (phi) i+sin (theta) sin (phi)j+cos (theta)k, with theata and phi shown in attachment given by
|+n> = cos (theta/2)|+z>+e^(i*theta) sin (theta/2)|-z>
a) Verify that the state |+n> reduces to the states |+x> and |+y> for angles theta and phi
b)Suppose that a measurement of S(sub z) is carried out on a particle in the state |+n> What is the probability that the measurement yields ((hbar)/2)? and ((-hbar)/2))
c) Determine the uncertainty (change of S(subz))of your measurements
#7 a) what is the amp to find a particle that is in the state |+n> from problem #3 with S(sub y)=hbar/2? what is the probability? check result by evaluating he probability for an appropriate chocice of hte angles phi and theta
b)What is the amp to find a particle that is in the state |+y> with S(sub n)=hbar/2? What is hte probabtility?
#8 Show that the state
|+n> = sin(theta/2)|+z>-e^(i(theta)) cos (theta/2)|-z>
satisfies <+n|-n>=0, where the state |+n> is given from #3 Verify that <-n|-n>=1
please help, any hints on how to start would be appreciated.
#3 the state of spin-1/2 particle that is spin up along the axis whose direction is specified by the unit vector n=sin (theta) cos (phi) i+sin (theta) sin (phi)j+cos (theta)k, with theata and phi shown in attachment given by
|+n> = cos (theta/2)|+z>+e^(i*theta) sin (theta/2)|-z>
a) Verify that the state |+n> reduces to the states |+x> and |+y> for angles theta and phi
b)Suppose that a measurement of S(sub z) is carried out on a particle in the state |+n> What is the probability that the measurement yields ((hbar)/2)? and ((-hbar)/2))
c) Determine the uncertainty (change of S(subz))of your measurements
#7 a) what is the amp to find a particle that is in the state |+n> from problem #3 with S(sub y)=hbar/2? what is the probability? check result by evaluating he probability for an appropriate chocice of hte angles phi and theta
b)What is the amp to find a particle that is in the state |+y> with S(sub n)=hbar/2? What is hte probabtility?
#8 Show that the state
|+n> = sin(theta/2)|+z>-e^(i(theta)) cos (theta/2)|-z>
satisfies <+n|-n>=0, where the state |+n> is given from #3 Verify that <-n|-n>=1
Attachments
Last edited: