The average value of S operator

[Viona]

TL;DR Summary

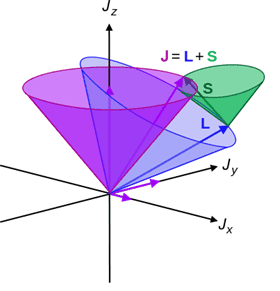
Why the average value of S operator is considered to be the projection of S onto J ?

While reading in the book of Introduction to Quantum Mechanics by David Griffith in the section of Fine structure of Hydrogen: spin- orbit coupling, he said that the average value of S operator is considered to be the projection of S onto J. I could not understand why he assumed that. please help me to understand.

 

[Twigg]

Given the fine-structure Hamiltonian $H = A\vec{L} \cdot \vec{S}$, try to calculate the commutator $[H,\vec{S}]$. What do you get, in vector form?

 

[Twigg]

What I was getting at is that if you do the algebra, I get $$[H,\vec{S}] = iA\vec{S} \times \vec{L} = iA\vec{S} \times \vec{J}$$ where the last step is true because $\vec{J} = \vec{L} + \vec{S}$. Use the Ehrenfest theorem on this to get $$\frac{d\langle \vec{S} \rangle}{dt} = \frac{A}{\hbar} \langle \vec{S} \times \vec{J} \rangle $$

$\vec{S}$ can be split into two components: $S_{||}$ which is parallel to $\vec{J}$ and $\vec{S}_{\perp}$ which is perpendicular to $\vec{J}$. Since the cross product cancels the parallel part, only the perpendicular part has time dependence (it precesses). The equation for $\langle \vec{S}_{\perp} \rangle$ is the equation for a spinning top (precession). The time averaged value of $\vec{S}_{\perp}$ is zero.

 

[Viona]

Thank you all for useful replies.