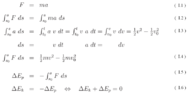The far reaching ramifications of the work-energy theorem

[Cleonis]

TL;DR Summary

By integrating $F=ma$ on both sides we obtain $\int_{s_0}^s F \ ds = \tfrac{1}{2}mv^2 - \tfrac{1}{2}mv_0^2$ That is already sufficient to imply conservation of mechanical energy

The work-energy theorem is the connection between expressing mechanics taking place in terms of force-and-acceleration, $F=ma$ and representing mechanics taking place in terms of interconversion of kinetic energy and potential energy.

The following statements are for the case that there is a single degree of freedom (motion along a single line) and that only a single force is acting.

To express the mathematics of the work-energy theorem the case of a single degree of freedom is sufficient. Using multiple degrees of freedom at this stage would be an instance of premature generalization.

\begin{array}{rcl}
ds & = & v \ dt \qquad \qquad(1.1) \\[+10pt]
a \ dt & = & dv \qquad \qquad(1.2) \\[+20pt]
F & = & ma \quad \qquad(1.3) \\[+10pt]
\int_{s_0}^s F \ ds & = & \int_{s_0}^s ma \ ds \qquad (1.4) \\[+10pt]
\int_{s_0}^s a \ ds & = & \int_{t_0}^t a \ v \ dt
= \int_{t_0}^t v \ a \ dt = \int_{v_0}^v v \ dv
= \tfrac{1}{2}v^2 - \tfrac{1}{2}v_0^2 \qquad (1.5) \\[+10pt]
\int_{s_0}^s F \ ds & = & \tfrac{1}{2}mv^2 - \tfrac{1}{2}mv_0^2 \qquad \qquad(1.6) \\[+10pt]
\Delta E_p & = & -\int_{s_0}^s F \ ds \qquad \qquad(1.7) \\[+10pt]
\Delta E_k & = & -\Delta E_p \quad \Leftrightarrow \quad \Delta E_k + \Delta E_p = 0 \qquad \qquad (1.8)
\end{array}This gives an overview of just how much purchase we get from $F=ma$

(1.4) performs the same operation both on the lelft hand side and the right hand side: integration with respect to the position coordinate, from $s_0$ to $s$.

(1.5) develops the integral of the acceleration with respect to the position coordinate. At this point the acceleration is unspecified, any differentiable acceleration is allowed. However, because acceleration and position are not independent of each other we can develop the integral nonetheless. (The steps of (1.5) use the relations (1.1) and (1.2); on changing the differential the limits of integration change accordingly.)

(1.6) is the work-energy theorem.

$F=ma$ and the work-energy theorem (1.6) have the same physics content. The integration and the subsequent development steps are all mathematical operations; they don't add physics content.

That is: the work-energy theorem is another way of expressing $F=ma$Potential energy
With the work-energy theorem established it is a no-brainer to define a concept of mechanical potential energy.

(1.7) gives the definition of mechanical potential energy.
From that definition it follows that for any change of mechanical potential energy there will be a matching change of kinetic energy: (1.8).
From that it follows that the sum of mechanical kinetic energy and mechanical potential energe will alway be a constant value.

We have, of course, that the definition stated in (1.7) is subject to a condition. The concept of potential energy is well defined only when the outcome of the integration is independent of how the object moves from start point to end point. Stated differently: for any path from start point to end point the outcome of the integration must be the same, otherwise the potential energy is not well defined.Overview:
Once $F=ma$ is granted (1.4) to (1.8) follow logically, no additional axiom required
That is a lot of ground covered.To recover F=ma

To return from energy representation to $F=ma$: do the inverse of what the derivation of the work-energy theorem does: take the derivative with respect to the position coordinate.

To recover the force from the potential energy we take the gradient of the potential energy. If there is only a single degree of freedom we simply take the derivative of the potential energy with respect to the position coordinate. If there are more degrees of freedom then the potential energe must be defined for each degree of freedom. Evaluating the gradient of the respective potential energy components then recovers the force as a vector.

To recover the acceleration from the kinetic energy we do the same: differentiation with respect to the position coordinate.
$$ \frac{d(\tfrac{1}{2}mv^2)}{ds} = \tfrac{1}{2}m\left( 2v\frac{dv}{ds} \right) = m\frac{ds}{dt}\frac{dv}{ds} = m\frac{dv}{dt} = ma \tag{2.1} $$
Incidentally, that is how in Mechanics the Euler-Lagrange equation recovers the $ma$ part of $F=ma$.
It looks as if it is a different operation, but the fact that it arrives at the same result shows that it is actually the same operation as (2.1):
$$ \frac{d}{dt} \frac{d(\tfrac{1}{2}mv^2)}{dv} = \frac{d}{dt}mv = ma \tag{2.2} $$Generalized coordinates

As we know, representation of mechanics taking place in terms of energy lends itself well to application of generalized coordinates. When the potential energy is expressed in some form of generalized coordinates the result of taking the derivative with respect to the position coordinate is generalized force

To any form of expressing a second derivative of position in applicable generalized coordinates there is a corresponding generalized force.

quoting from the already linked to discussion by Richard Fitzpatrick:

Here, the $Q_i$ are termed generalized forces. More explicitly, $Q_i$ is termed the force conjugate to the coordinate $q_i$ . Note that a generalized force does not necessarily have the dimensions of force. However, the product $Q_i q_i$ must have the dimensions of work. Thus, if a particular $q_i$ is a Cartesian coordinate then the associated $Q_i$ is a force. Conversely, if a particular $q_i$ is an angle then the associated $Q_i$ is a torque.

Application in other areas of physics
The pattern of the derivation, the steps from (1.4) to (1.6), is applicable for other physics phenomena. In the process the concept of Energy is generalized to areas beyond Mechanics.

Example: the electrodynamics of an LC circuit.

As we know: electric oscillation in an LC circuit is analogous to mechanical oscillation. The simplest case of mechanical oscillation is when the restoring force is according to Hooke's law.

$V$ voltage (electromotive force)
$I$ current in the circuit (charge through the circuit per unit of time)
$L$ Inductance (counterpart of inertia)
$C$ Capacitance

In the case of an LC circuit: the simplest case is:
A capacitance such that the electromotive force increases linear with the amount of accumulated charge
An inductance such that the relation between electromotive force and time derivative of $I$ is linear.

Richard Fitzpatrick gives for the total energy in the case of electric oscillation in an LC circuit:
$$ E = \tfrac{1}{2} CV^2 + \tfrac{1}{2}LI^2 \tag{3.1} $$
The expression for the energy of the current $I$ is proportional to the square of the current $I$ because change of current is the second time derivative of charge through the circuit.We have that mechanical motion can be converted to electric motion; a dynamo generates electromotive force. We find experimentally that the conversion rate is consistent; with all forms of intermediate loss accounted for the conversion rate is always the same. Moreover, we can convert energy form A to B, B to C, and when converting back from C to A the original amount of energy is recovered.

Of course, that is what led to the supposition of universal validity of conservation of energy.

Perception of the work-energy theorem in the physics community

I get the impression that some textbook authors do not appreciate the relevancy of the work-energy theorem.

Example:
On the website 'Hyperphysics' there is a link to:
work-energy principle

The Work-Energy Principle [...] is often a very useful tool in mechanics problem solving. It is derivable from conservation of energy and the application of the relationships for work and energy, so it is not independent of the conservation laws. It is in fact a specific application of conservation of energy.

The reader may get the impression that the work-energy relation is independent from $F=ma$

There is a separate page with some remarks about kinetic energy:
More Detail on Kinetic Energy Concept
But the remarks there do not amount to a derivation

 

[PeterDonis]

I grouped the following 6 equations in an image because that gives me more control over the alignment than I have with MathJax/LaTeX

Sorry, but this is not acceptable. There are ways in LaTeX to align equations.

The work-energy theorem

What is the purpose of this post? Do you have a question about the work-energy theorem? Are you trying to derive some significant result?

 

[Dale]

1.3 is a little wrong. It should be $\Sigma F= ma$ or $F_{net}=ma$. The way 1.3 is written is a common way of verbally stating Newton’s 2nd law, but in a proof you should write it correctly.

This incorrect writing causes problems in 1.7, which is questionable anyway.

I am not a fan of the work energy theorem. It is usually taught and derived in a way that substantially confuses new students.

 

[Cleonis]

Sorry, but this is not acceptable. There are ways in LaTeX to align equations.

I have replaced the image with MathJax/LaTeX.
To make up for the unnumbered line in the image version I stated those relations as (1.1) and (1.2)

(I tried to replicate the layout of the image version with LaTeX syntax, so far no luck.)

 

[Cleonis]

What is the purpose of this post? Do you have a question about the work-energy theorem? Are you trying to derive some significant result?

Among the purposes of the post is to probe what in general the attitude is (among the readers of the 'classical physics' forum) towards the work-energy theorem.

I am of the opinion that there are no new results in the narrative that I present.
Different authors derive the work-energy theorem in different ways, but of course they all arrive at the same result: the work-energy theorem. I present a sequence of steps that arrives at the work-energy theorem.

In general it is not unusual that for a particular theorem multiple different derivations are in circulation. The most pronounced example of that is Pythagoras' theorem. I just googled it; there is a book with over 300 proofs of Pythagoras' theorem.

It may well be that the particular form of the work-energy theorem derivation that I give here is not present in the literature in that exact form, but it seems to me that should not count against it.

In my post I follow straightforward logical implication.

I am aware of the physicsforum policy of not being a platform for original research. I argue that what I wrote does not constitute new results.

 

[vanhees71]

The prime sin in teaching mechanics is, not to use vectors! I'm sorry to say that #1 is an example for that rule!

 

[Cleonis]

I am not a fan of the work energy theorem. It is usually taught and derived in a way that substantially confuses new students.

Then by all means the work-energy theorem should be taught in a way that minimizes the likelyhood of confusing new students.Many sources use Torricelli's equation to supply the relation between acceleration, displacement, and change of velocity:

$v_i$ initial velocity
$v_f$ final velocity
$s_i$ initial position
$s_f$ final position
$a$ acceleration
$$ a (s_f - s_i) = v_f^2 - v_i^2 $$
One disadvantage of that: the derivation of Torricelli's equation is for the case of uniform acceleration.
So after using Torricelli's equation you still have to generalize to non-uniform acceleration.

Still, for new students it is probably better to introduce the work-energy theorem by way of Torricelli's equation.

The purpose of the derivation that I gave in my post is to be an efficient derivation, for an audience of readers who are comfortable with the integration and differentiation operations that are used.

I am strongly influenced by the style of math exposition that Grant Sanderson uses. Start with the simplest case that manifests the property that you want to show, and from there generalize stage by stage.

 

[Cleonis]

The prime sin in teaching mechanics is, not to use vectors! I'm sorry to say that #1 is an example for that rule!

I am very eager to address this.

Among the standard tools of classroom demonstration is an air track.

(And nowadays, if the school does not have the money to buy an air track, the students making their first steps into Mechanics can watch air track demonstrations via internet connection.)

I am strongly influenced by the style of exposition that Grant Sanderson uses. Start with the simplest case that manifests the property that you want to show, and from there generalize stage by stage.

The student is introduced to the concept of conservation of momentum by watching two gliders collide. (We know the range of possibilities: make the gliders stick together, or make them bounce them of each other, etc.)

The very physical implementation of the airtrack constrains the motion to a single degree of freedom. Because of that: it is at that stage not necessary to introduce vectorial notation.

Within the context of a single degree of freedom already a lot of ground can be covered. Once that is accomplished the teacher shows how to generalize to two and more degrees of freedom.

I believe that for most subjects that we want to teach to the students there is a natural staging. I believe premature generalization reduces the effectiveness of the teaching effort.I see why it is tempting for a teacher to throw in vectorial notation from the start; the student is going to need it soon anyway, so let's put it up front. But I believe that on balance premature generalization is disadvantageous.Later edit:
Granted, even with a single degree of freedom: velocity and acceleraton are vectorial in the sense that you have to keep track of positive direction and negative direction. As in: if I lose a minus sign I'm in trouble.

 

[Cleonis]

I am not a fan of the work energy theorem. It is usually taught and derived in a way that substantially confuses new students.

I'm writing a second reply to the same remark.

When I see some online available resource (a textbook, lecture notes) I check out whether the author introduces the work-energy theorem, and if so, how.

Many authors do not introduce the work-energy theorem at all, and the ones that do often give a haphazard sequence of steps. I can easily see how a student can feel he is being bamboozled.In my derivation in post #1 I put emphasis on structure.
There is the symmetry of performing the same operation on the left hand side and the right hand side (1.4)
Why is it that (1.5) can be developed? That is because position and acceleration are not independent.
Acceleration is two differentiation steps away from position. The derivation that I present demonstrates symmetry: the initial expression is in terms of acceleration and position. Those two are the outer elements of the trio: position, velocity, acceleration.
The final integral expression, $\int_{v_0}^v \ v \ dv$, is an integral expression purely in terms of velocity, the middle element of the three.

 

[Dale]

Then by all means the work-energy theorem should be taught in a way that minimizes the likelyhood of confusing new students.

Many authors do not introduce the work-energy theorem at all, and the ones that do often give a haphazard sequence of steps. I can easily see how a student can feel he is being bamboozled.

Your derivation makes the same mistakes and causes the same problems as all of the others. You are just throwing symbols around without regard for the physics. To me, this is why most presentations are "haphazard", and this is not different.

All useful derivations of some physics formula start with a set of clearly stated assumptions, a clear restriction of what scenario or range of scenarios is being discussed.

Your derivation does not. Is this intended for a point particle, a rigid body, or a deformable object? Is the object acted on by a single force or multiple forces? Does it apply if the force is non-conservative? What do each of the symbols mean?

The derivation you present, along with all of the other derivations I dislike, does not discuss the limitations of the derivation. It does not give the student guidance on when it applies and when it does not apply. It doesn’t tell the student the physical meaning of the terms.

 

[Dale]

Let me explain an issue or two that arises with your derivation and similar when students go to apply it in a couple of scenarios:

1) skydiver falling at terminal velocity. Since they are at terminal velocity $\Delta E_k=0$ and so by 1.8 $\Delta E_p=0$. However, students will have also been taught that $\Delta E_p=mg\Delta h \ne 0$. This will cause confusion since there is a change in PE but no change in KE and the way that you have presented the work energy theorem that should not happen.

2) car accelerating on flat ground without air resistance. Since $\Delta E_k>0$ then $-\Delta E_k=\Delta E_p<0$. But the only external force is the friction force. This will cause confusion because it looks like the friction force does positive work (where did it get the energy and how) and because it looks like the friction force is associated with a potential energy (but it is a non-conservative force).

Far more important than the steps of the derivation is a clear presentation on the meaning of the terms and the resulting equations. And equally important is a clear presentation on the restrictions, assumptions, and limitations of the derivation. If you are going to teach the work energy theorem at all then you should do so in a way that includes all information students need to be able to apply it correctly.

 

[weirdoguy]

And equally important is a clear presentation on the restrictions, assumptions, and limitations of the derivation.

Do you know any textbook that does that the best way?

 

[Dale]

Do you know any textbook that does that the best way?

No. I have never seen any textbook give a good presentation of the work-energy theorem.

 

[vanhees71]

Well, I think it's pretty simple (at least for the simple case of a particle moving in an external force field). Just write down Newton's equation of motion
$$m \ddot{\vec{x}}=\vec{F}(t,\vec{x}).$$
Then take the scalar product of this equation of motion by $\dot{\vec{x}}$ and integrate between two times $t_1$ and $t_2$. Then you get
$$T_2-T_1=\int_{t_1}^{t_2} \mathrm{d} t \vec{F}(t,\vec{x}(t)) \cdot \dot{\vec{x}}(t),$$
where $\vec{x}(t)$ is a solution of the equation of motion and $T=m \dot{\vec{x}}^2/2$ and $T_{1/2}$ the values of this "kinetic energy" at times, $t_1$ and $t_2$

The latter point makes the "work-energy theorem" pretty empty, because you have to know the solution before you can use this theorem.

Things change, if there's a potential such that $\vec{F}(\vec{x})=-\vec{\nabla} V(\vec{x})$, i.e., if $\vec{F}$ is not explicitly time dependent and if it has a potential. Then the right-hand side of the work-energy theorem becomes independent of the path connecting the initial and final points, and you have
$$T_2-T_1=-(V_2-V_1) \; \Rightarrow \; T_2+V_2=T_1+V_1=E,$$
i.e., in this case you know that energy is conserved along any trajectory of the particle. You don't need to know this trajectory before applying this energy-conservation law.

 

[robphy]

[snip]

(1.7) gives the definition of mechanical potential energy.
From that definition it follows that for any change of mechanical potential energy there will be a matching change of kinetic energy: (1.8).
From that it follows that the sum of mechanical kinetic energy and mechanical potential energe will alway be a constant value.

[snip]

We have, of course, that the definition stated in (1.7) is subject to a condition. The concept of potential energy is well defined only when the outcome of the integration is independent of how the object moves from start point to end point. Stated differently: for any path from start point to end point the outcome of the integration must be the same, otherwise the potential energy is not well defined.

To me, a good presentation of the work-energy theorem

• begins with Newton's Second Law (with $\vec F_{net}=m \vec a$ ;
  leaving out "net" invites possible misconceptions
  that each force has its own acceleration or has its own change to the kinetic energy)
• then, "kinetic energy" is then clearly defined here (not pre-supposed from elsewhere)
• then, expresses the "net work" as the sum of the
  "work due to conservative forces" plus "work due to nonconservative forces" $W_{net}=W_{cons}+W_{nc}$ (while clearly explaining the partition)
• then, "potential energy" is then clearly defined here for only conservative forces (not pre-supposed from elsewhere)... [ "of course" pre-supposes an understanding that a novice will likely not immediately appreciate]. The minus-sign must be clearly explained.
• "conservation of total mechanical energy" holds when $W_{nc}=0$ for any path
• The logic must be as clear as possible.
  I would rewrite some of what you have written as
  $$\begin{array}{rcl}
  \int_{s_0}^s F_{net,s} \ ds
  & \stackrel{Newton II}{=} & \tfrac{1}{2}mv^2 - \tfrac{1}{2}mv_0^2 \qquad \qquad(1.6) \\
  W_{cons} + W_{nc}& = & \Delta E_k\qquad\qquad(1.6b) \\
  (-\Delta E_p) + W_{nc}& = & \Delta E_k\qquad\qquad(1.7)\\
  W_{nc}& = & \Delta E_k- (-\Delta E_p)\qquad\qquad(1.7b)\\
  0& \stackrel{W_{nc}=0}{=} & \Delta E_k + \Delta E_p \qquad(1.8)
  \end{array}$$

 

[Dale]

then, expresses the "net work" as the sum of the
"work due to conservative forces" plus "work due to nonconservative forces" $W_{net}=W_{cons}+W_{nc}$ (while clearly explaining the partition)

Unfortunately this is either incorrect or confusing/misleading for a student.

Consider an electric car accelerating at a constant rate on a level road with negligible losses (air drag, rolling resistance, electrical losses). The “net work” is equal to the distance that the center of mass moved times the static friction force. However, the work done by static friction is 0. No other external forces, either conservative or non-conservative, do any work either. So this equation is transferred either in or out of the car.

In fact, no work is done on the car. The energy of the battery is converted into kinetic energy, so the total energy of the car is constant. No energy is transferred and work is a transfer of energy (by any means other than heat).

Unfortunately, the “net work” terminology is pretty standard, and I dislike it precisely because people think that it is the sum of the work from each force acting on the system. It is not. It is the net force times the distance that the center of mass moved. It has units of work but does not represent the total work done on an object. The “net” in “net work” refers to the “net force”, not to some sum of works.

I would prefer to call it “center of mass work”, since it is related to the motion of the center of mass. But that terminology is not going to change. Instead I could introduce the “thermodynamic work” which is the sum of the work done by all forces acting on a system. If you classify the forces as conservative and non-conservative then $$W_{net}\ne W_{thermo}=W_{cons}+W_{nc}$$

 

[robphy]

Unfortunately this is either incorrect or confusing/misleading for a student.

[snip]

Unfortunately, the “net work” terminology is pretty standard, and I dislike it precisely because people think that it is the sum of the work from each force acting on the system. It is not. It is the net force times the distance that the center of mass moved. It has units of work but does not represent the total work done on an object. The “net” in “net work” refers to the “net force”, not to some sum of works.

I would prefer to call it “center of mass work”, since it is related to the motion of the center of mass. But that terminology is not going to change. Instead I introduce the “thermodynamic work” which is the sum of the work done by all forces acting on a system. If you classify the forces as conservative and non-conservative then $$W_{net}\ne W_{thermo}=W_{cons}+W_{nc}$$

Yes, I would agree.
However, in the typical sequence,
the implicit assumption is that
the work-energy theorem is introduced when
we are dealing with "point particles" (rather than a system of particles)
and the typical mechanical forces [gravity, tension, friction, normal force, spring-force].

In the typical kinematics-force-energy-momentum sequence,
neither "center of mass" nor "thermodynamic work" is not yet introduced.
As usual,
when the situation is more developed
(e.g. with a system of particles or with thermodynamics),
one often revises, extends, and clarifies the initial formulation in a simple situation,
rather than initially formulating something to cover the general situation.
(Indeed, we typically don't develop "relativistic kinetic energy" when introducing work-energy.)

So, along the lines of all of these discussions,
the assumptions probably need to be stated
so that one understands the range of applicability of the theorem (as stated).

Some more modern texts, like Matter and Interactions (by Chabay and Sherwood)
and Six Ideas That Shaped Physics (by Moore),
introduce momentum and systems of particles before kinetic-energy.
In those textbooks, their initial treatment of "work"
(with more refined notions of "pseudowork" and "k-work" in their earlier editions)
is more along the lines you describe.

 

[Dale]

the implicit assumption is that
the work-energy theorem is introduced when
we are dealing with "point particles" (rather than a system of particles)

Honestly, that is probably the main reason that I have never seen a good presentation of the work energy theorem in any textbook. A restriction like that is important enough to justify making that assumption explicit. That way students would understand why it fails in these cases.

one often revises, extends, and clarifies the initial formulation in a simple situation

I haven’t seen that done either for the work energy theorem. That would be acceptable.

In the typical kinematics-force-energy-momentum sequence,
neither "center of mass" nor "thermodynamic work" is not yet introduced.

That isn’t an issue. It can be simply defined and given that name “for reasons that will become clear in …”

Some more modern texts, like Matter and Interactions (by Chabay and Sherwood)
and Six Ideas That Shaped Physics (by Moore),
introduce momentum and systems of particles before kinetic-energy.
In those textbooks, their initial treatment of "work"
(with more refined notions of "pseudowork" and "k-work" in their earlier editions)
is more along the lines you describe.

That sounds interesting. And I do like the term “pseudowork”.

 

[cianfa72]

Unfortunately, the “net work” terminology is pretty standard, and I dislike it precisely because people think that it is the sum of the work from each force acting on the system. It is not. It is the net force times the distance that the center of mass moved. It has units of work but does not represent the total work done on an object. The “net” in “net work” refers to the “net force”, not to some sum of works.

From the sources I studied on (see for instance here), the work-energy theorem for a system of particles (i.e. a system that can have internal degree of freedom) claims that the total work done from external forces (external w.r.t. the system) on the system equals its change of total energy. Of course both external work and system's energy are evaluated in a given inertial frame (they are not frame invariant).

Note that the external work is not the line integral of the external "net force" times the displacement of system's center of mass.

This way work-energy theorem describes also the "external energy" transferred by external work on the system possibly stored in system's (internal) potential energy (if it has internal degree of freedom).

 

[Dale]

Note that the external work is not the line integral of the external "net force" times the displacement of system's center of mass.

This is what I call “total work” to distinguish it from the “net work”. One difficulty is that different authors use different terminology.

work-energy theorem for a system of particles

I have a basic aversion to classical point particles. So I do not use them.

However, I do find that generally the authors that use classical point particles, those authors tend to do a more accurate job of presenting the work energy theorem. I agree that what you have described is correct, just not an explanation I would use due to my objection to classical point particles.

 

[cianfa72]

I have a basic aversion to classical point particles. So I do not use them.

Why do you have such aversion ?

 

[Dale]

Why do you have such aversion ?

All of the problems with classical mechanics that I am aware of come from classical point particles. They don’t exist experimentally and they cause problems theoretically, so I avoid them

 

[cianfa72]

All of the problems with classical mechanics that I am aware of come from classical point particles. They don’t exist experimentally and they cause problems theoretically, so I avoid them

Yes, I see. However I believe there are circumstances where this cannot be avoided (e.g. billiard balls collision analysis).

 

[Dale]

Yes, I see. However I believe there are circumstances where this cannot be avoided (e.g. billiard balls collision analysis).

If you treat billiard balls as point particles then you will get a lot of near misses that should be collisions. Billiard balls are better treated as rigid spheres than as point particles.

 

[cianfa72]

If you treat billiard balls as point particles then you will get a lot of near misses that should be collisions. Billiard balls are better treated as rigid spheres than as point particles.

Yes of course, but if you treat them as rigid spheres then which formulation of Newton's laws you use for a such system of macroscopic bodies ?

 

[Dale]

if you treat them as rigid spheres then which formulation of Newton's laws you apply for a such system of macroscopic bodies ?

The usual one. One based on “bodies” or “systems” rather than particles.

 

[cianfa72]

The usual one. One based on “bodies” or “systems” rather than particles.

Ok, so for example for a "two bodies interacting system" the Newton's 3th law on force pairs between the two bodies (and not between point particles having zero extent/volume).

 

[PeterDonis]

so for example for a "two bodies interacting system" the Newton's 3th law on force pairs between the two bodies (and not between point particles having zero extent/volume).

For many scenarios the two are the same. Newton proved a theorem that, if you're not concerned with anything internal to the bodies, and the bodies are spherical, the gravitational force between them is the same as if they were point particles. So the method @Dale describes ends up being the same, mathematically, for many scenarios as the point particle method--but now recognizing the actual domain in which the method works.

 

[cianfa72]

For many scenarios the two are the same. Newton proved a theorem that, if you're not concerned with anything internal to the bodies, and the bodies are spherical, the gravitational force between them is the same as if they were point particles.

Yes, but what about electromagnetic force pairs ? The same rule/theorem applies also for them ?

 

[PeterDonis]

Yes, but what about electromagnetic force pairs ? The same rule/theorem applies also for them ?

For EM, I believe there is a similar theorem for spherical charge distributions, yes.

 

[cianfa72]

This is what I call “total work” to distinguish it from the “net work”. One difficulty is that different authors use different terminology.

Sorry, just to be pedantic I would say "total external work" to highlight that the work of internal forces (Newton's 3rd pairs) is not included.

 

[Dale]

Sorry, just to be pedantic I would say "total external work" to highlight that the work of internal forces (Newton's 3rd pairs) is not included.

I never deal with internal forces. So for me that is unnecessary.