The Lagrangian for a piece of toast falling over the edge of a table

[Markus Kahn]

Homework Statement

The ultimate goal is to find the equations of motion for a piece of toast falling from a table.

Relevant Equations

Euler-Lagrange equations.

First of all, disclaimer: This isn't an official assignment or anything, so I'm not even sure if there is a resonably simple solution.

Consider the following sketch.

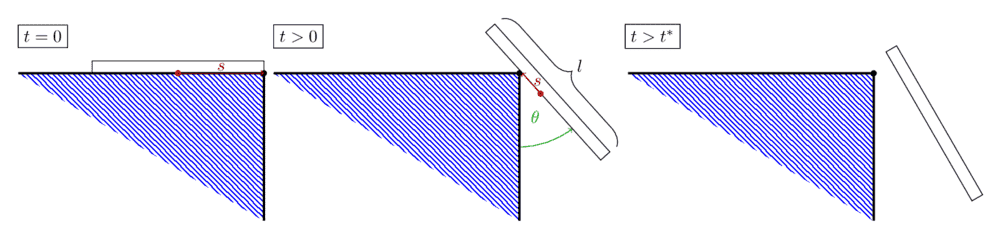
(Forgive me if it isn't completely clear, I didn't want to fiddle around for too long with tikz...)

Let us assume that we can approximate a piece of toast as a rectangle with homogenous mass distribution $m$ and length $l$. We further assume that for $t=0$ the toast has velocity in positive $x$ direction. We can describe the system over the two generalized coordinates $s$ and $\theta$, where $s$ gives the distance from the center of mass to the coordinate frame center (let us for now assume that the toast is infinitely thin... Not sure if this is necessary though) and $\theta$ beeing the angle between the toast and the $y$ axis. We can then write for the center of mass
$$\vec{x}_p = s(t)\begin{pmatrix}\sin(\theta(t))\\-\cos(\theta(t))\end{pmatrix}.$$
We find therefore for the kinetic and potential energy
$$T=\frac{1}{2}m\dot{x}_p^2 = \frac{1}{2}m (\dot s ^2 + s^2\dot \theta^2)\quad\text{and}\quad V=-mg s\cos(\theta),$$
which therefore would result in the following Lagrange function
$$L = \frac{1}{2} m (2 g \cos(\theta(t)) s(t) + \dot s(t)^2 +
s(t)^2 \dot \theta (t)^2).$$
Is this correct up until here? Finding the eom's isn't really a problem if this is correct..

PS: the third picture should just indicate that one can find $t^*$ with the condition $(\ddot{x_p})_x\overset{!}{=}0$ for which the toast loose its contact to the table.

 

[Orodruin]

Your kinetic energy is not correct. You are missing the moment of inertia around the center of mass.

 

[Markus Kahn]

Thanks, completely forgot about that part... In that case we have
$$T= \frac{1}{2}m (\dot s ^2 + s^2\dot \theta^2)+ \frac{1}{2}I_{(0,0)} \dot\theta^2,$$
where $I_{(0,0)}$ is the moment of inertia in respect to the center of the coordinate frame. With the parallel axis theorem we have
$$I_{(0,0)} = \frac{1}{12}ml^2 + ms^2\Longrightarrow T = \frac{1}{2}m\dot s^2 + \frac{1}{24}ml^2\dot\theta^2 + s^2\dot\theta^2 .$$

 

[wrobel]

I do not think that the solution to corresponding Lagrange equations is available in closed form

 

[Markus Kahn]

Me neither, so I just decieded to try it numerically but I'm already running into problems.. Mainly due to the fact that the condition I wanted to use to determine $t^*$ doesn't really lead to anything. If I calculate the second derivative of the $x$-component of $x_p$ I get
$$(\ddot{x}_p)_x = \sin(\theta(t)) (\ddot s(t) - s(t) \dot\theta(t)^2) + \cos(\theta(t)) (2 \dot s(t) \dot\theta(t) + s(t)\ddot\theta(t))\overset{!}{=}0 $$
but Mathematica tells me that there are no zero values for this function (for the numerical solutions I obtained..)

 

[Markus Kahn]

Alright, I'm doing something wrong and I can't figure out what it is.. As established above the Lagrangian is given by
$$L = \frac{1}{2}m\dot s^2 + \frac{1}{24}ml^2\dot\theta^2 + ms^2\dot\theta^2 + mg s \cos(\theta) . $$
We therefore have
$$
\begin{align*}
\frac{\partial L}{\partial s} &= 2s\dot\theta ^2m + mg\cos\theta&\quad \frac{\partial L}{\partial\dot s} &= m\dot s & \quad \frac{\partial L}{\partial \theta} &= -mgs \sin\theta &\quad \frac{\partial L}{\partial\dot \theta} &= \frac{1}{12}ml^2\dot\theta + 2ms^2\dot\theta.
\end{align*}
$$
We can now go on and calculate
$$
\begin{align*}
\frac{d}{dt} \frac{\partial L}{\partial \dot s}&= m\ddot s\\
\frac{d}{dt} \frac{\partial L}{\partial \dot \theta}&= \frac{1}{2}ml^2\ddot \theta + 2m \frac{d}{dt}(s^2\dot\theta) = \frac{1}{2}ml^2\ddot \theta + 2m(2s\dot s \dot \theta +s^2\ddot\theta) = \frac{1}{2}ml^2\ddot \theta +4s\dot s \dot\theta + 2ms^2\ddot\theta
\end{align*}
$$
We therefore get the two eom's
$$
\begin{align*}
2s\dot\theta^2 +g \cos\theta &=\ddot s \\
l^2\ddot\theta + 48 s \dot s \dot\theta + 24s^2\ddot\theta + 12 gs\sin\theta &=0
\end{align*}
$$
Solving this numerically isn't really an issue and plotting the trajectory with inital values
$$s(0)=l/2,\quad \dot s(0)= 0.3,\quad u(0)= \pi /2,\quad \dot u(0)= -0.1$$
gives

and if I plot $(\ddot x_p)_x$ I get this (cannot upload second image directly...). I don't really see how this can be.. At some point $(\ddot x_p)_x$ needs to be zero for the bread to lose contact to the table, but apparently this doesn't happen.. Can someone explain this?