DavidBalut
- 3
- 0
- TL;DR Summary
- I am trying to understand Minkowski diagrams.
Hello,
My name is Dave and I'm a physics major at UIUC. It looks like I will be taking the special relativity course (phys 225) this fall. I've always been fascinated by the theory so I decided to get a head start with Lenny and Art's perspective on it.
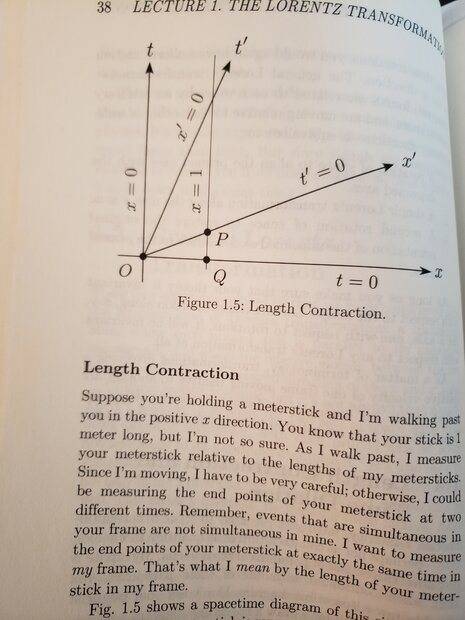
My first head-scratching moment came in section 1.4. First with the "geometry" of length contraction. I completely agree that on pg 38 the line OP is shorter than line OQ, due to the transforming coordinate Q onto the x prime axis in the form of point P. However, what I can't get my mind around is the "geometry of this situation" how can the "leg of a right triangle" be longer than the "hypotenuse of a right triangle"
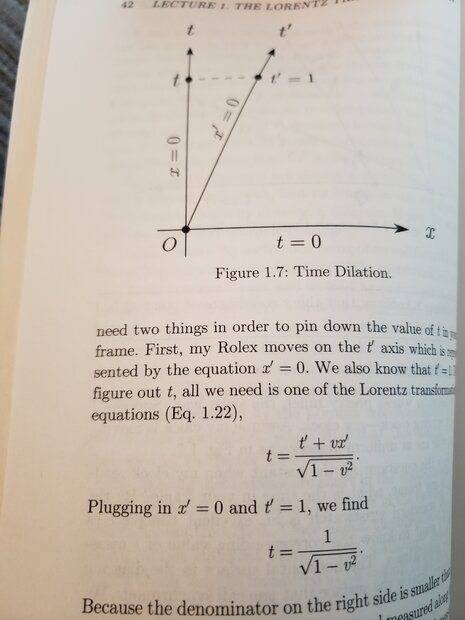
This happens again on page 42. Time moves slower in the moving frame such that t_stationary frame > t_moving frame. Yet, once again the leg is greater than the hypotenuse.
I have a feeling that apparent lengths on different axes are irrelevant and arbitrary and what really matters is calculated values by Lorentz transformations.
Any help is greatly appreciated!
My name is Dave and I'm a physics major at UIUC. It looks like I will be taking the special relativity course (phys 225) this fall. I've always been fascinated by the theory so I decided to get a head start with Lenny and Art's perspective on it.
My first head-scratching moment came in section 1.4. First with the "geometry" of length contraction. I completely agree that on pg 38 the line OP is shorter than line OQ, due to the transforming coordinate Q onto the x prime axis in the form of point P. However, what I can't get my mind around is the "geometry of this situation" how can the "leg of a right triangle" be longer than the "hypotenuse of a right triangle"
This happens again on page 42. Time moves slower in the moving frame such that t_stationary frame > t_moving frame. Yet, once again the leg is greater than the hypotenuse.
I have a feeling that apparent lengths on different axes are irrelevant and arbitrary and what really matters is calculated values by Lorentz transformations.
Any help is greatly appreciated!