Time to empty gas cylinder (problem worked, but would like feedback)

[Danild]

TL;DR Summary

I am trying to calculate the time it takes to empty a cylinder with gas into atmospheric pressure.
(I have general idea, but need feedback if solution is good)

Hi everyone

I am trying to solve a specific problem. I already have an idea on how to solve it, but I hoped someone else could tell me if my general approach is somewhat sensible or not. So I would really appreciate some feedback.

Situation:
A long, narrow cylinder filled with gas that is at higher pressure than atmospheric. (like for example a cylinder that is 0.01 meters in diameter, and 10 meters long, and the absolute pressure is 4 bar / 400kPa.
Now we open the cylinder in one end, and the overpressurized gas will empty out into the atmospheric air.
The opening will be big compared to the cylinder, like for example 0.008 m in diameter.
What I am trying to solve:
When will the pressure in the cylinder have dropped to around 108 kPa (assuming atmospheric pressure of around 103 kPa)?

---My general idea sofar---

Overall calculation method:
I realize that this is a non-stationary problem, which complicates things a lot. I am planning to use a Python script, that runs through all the calculations continously, at very small time-increments, like for example 1/100 or 1/1000 of a second, or even smaller. I am hoping that the error I make will become rather small if I do this.
I am not expecting a precise result, to be honest if I can just get within an error margin of 20% I will consider it quite a success!

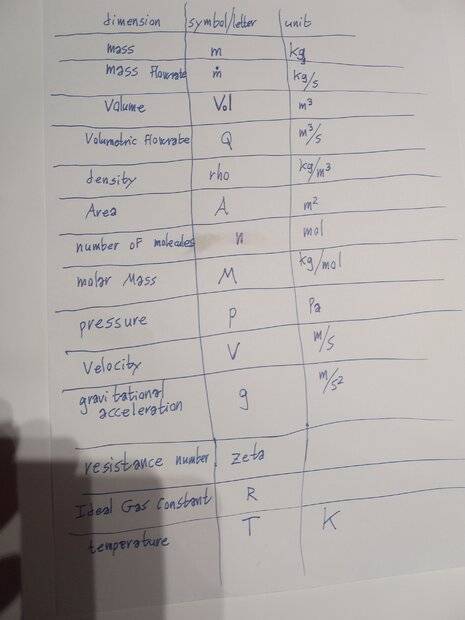
Known values:
Size of container and size of opening. Pressure and temperature inside and outside of cylinder. Molar mass of the gas (in this case regular air).

Formulas/concepts used:
Energy Equation (basically just Bernoullis Equation but with energy-losses added) (geometric height cancels out, since cylinder is horisontal, and geometric height-differences are negligible)
Ideal Gas Law
Conservation of mass (concept).

Assumptions:
Velocities is assumed to be below the speed of sound, Mach Number < 1
Constant temperature (however I might want to expand the calculations to include this too, after I have nailed this first part).I decided to carefully hand-write my formula-gymnastics, and take a picture, in the hope that they will be easier for you to read than a typed up version:

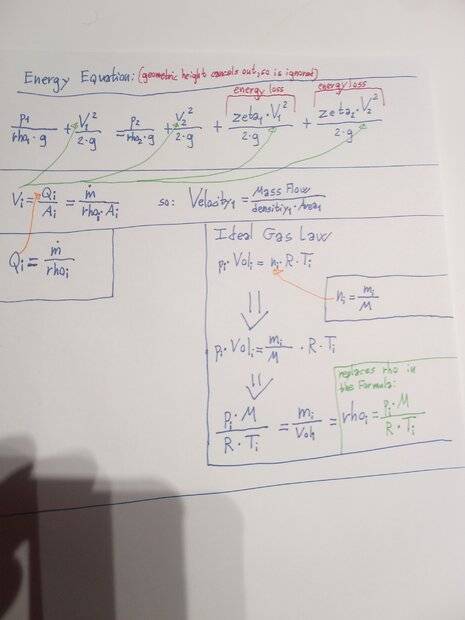
(Note: The resistance numbers I am referring to is simply going to be looked up on a table, based on the geometry of the opening)

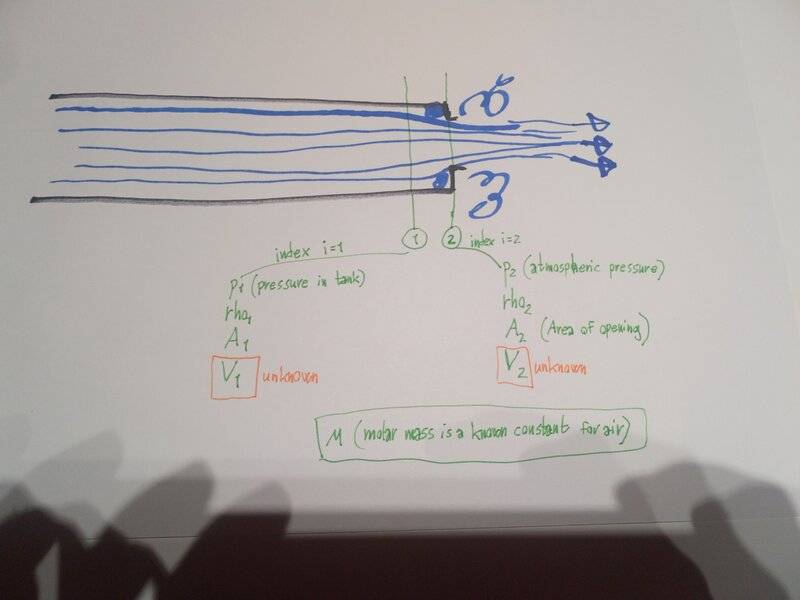
As you can see from my scetch, I am using an energy-equation (similar to Bernoulli), and comparing 2 points, with index 1 and index 2.
Index 1 is inside the cylinder, just far enough inside that the flow hasn't started contracting yet towards the opening.
Index 2 is just at the end of the opening, so I am assuming atmospheric pressure at this point.
The problem is that I have an unknown speed at both Index 1 and Index 2 (two unknowns), and I cannot assume the same volumetric flow at both points, because the densities are changing.
I can however assume Conservation of mass, and by converting the velocities to mass-flows, I solve both of these problems.

The idea is then to calculate the mass flow at the starting point, calculate the mass "lost" from the cylinder during a small period of time (1/1000 second or similar), and then recalculate internal pressure based on this new total mass, and then start over again with a new mass-flow calculation, and so on in a loop, until some predetermined pressure has been reached.What do you think? Am I on the right track, or did I make some mistakes in my basic thinking and assumptions?

 

[osilmag]

You've put a lot of effort into this. Are there too many unknowns to find your mass flow?

 

[erobz]

I think rapid expansions like this are theoretically tough to deal with. I’ve heard @Chestermiller state you shouldn’t ignore viscosity, and there is always speculation about how well the ideal gas assumption works because of the flow being well outside of “passing through equilibrium states”. Also, the flow is unsteady, and the “Energy Equation” is derived under the steady flow assumption. Many things to consider.

Anyhow, are you also ignoring the temperature change?

 

[jack action]

It is so much more complicated than that. You cannot ignore the compressibility effects and cannot assume that velocity won't reach the speed of sound. All of the concepts involved are too complicated to explain simply in this thread. You will also have pressure waves reflected through your cylinder coming back to assist the outflow at the restriction.

I did solve a similar problem in the past - flow through an engine valve between a cylinder and a pipe. Here are the results put graphically for the Mach numbers in the restriction and the pipe:

Where:
$$Ar = \frac{A_{rest}}{A_{pipe}}$$
$$Y = \left(\frac{1}{2.7908k-2.795488}\right)\left(\frac{2X_{pipe\ 0}-1}{X_{cyl}}-1\right)$$
Furthermore:
$$X_n = \left(\frac{p_n}{p_{ref}}\right)^{\frac{k-1}{2k}}$$
$A_n$ is the area of $n$, $k$ is the specific heat ratio (the presented equation for $Y$ is valid for $1.2 \leq k \leq 1.45$), and, in your case, the reference pressure would be the atmospheric pressure which is the "cylinder" pressure as well. ($p_{ref} = p_{cyl} = p_{atm}$)

Your case would represent a positive value for $Y$. A negative value would mean the flow would be from the atmosphere (the "cylinder") to your pipe. The mass flow rate through the restrictor would be:
$$\dot{m} = \rho_{rest}v_{rest}A_{rest} = p_{atm}{X_{rest}}^\frac{k+1}{k-1}\sqrt{\frac{k}{RT_{pipe\ 0}}}M_{rest}A_{rest}$$
$R$ being the specific gas constant and $p_{rest} = p_{cyl}$ (meaning $X_{rest} = 1)$ if $M_{rest} < 1$. If $M_{rest} = 1$ then:
$$X_{rest} = \frac{\frac{2}{k-1} \left(2X_{pipe\ 0}-1\right)}{\frac{2}{k-1} + M_{pipe}} \left(M_{pipe}\frac{A_{pipe}}{A_{rest}}\right)^\frac{k-1}{k+1}$$
This work was done based on the theory found in Design and Simulation of Four-Stroke Engines by Gordon P. Blair.

I'm leaving off the equations for calculating the reflected pressure which would just be too much and useless without a more complex and lengthy context explained.

So assuming the initial conditions $Ar = 0.80$ and $\frac{p_{pipe\ 0}}{p_{ref}} = 4$ (then $Y = 0.394$), you should have a choked flow with $M_{rest} = 1$, $M_{pipe} \approx 0.56$ and $X_{rest} = 1.2186$. (So $p_{rest}$ is basically equal to the pressure in the pipe.)

Edit: I now realize that $Ar = 0.64$ in your case, meaning $M_{pipe} \approx 0.41$ and $X_{rest} = 1.234$.

 

[Danild]

You've put a lot of effort into this. Are there too many unknowns to find your mass flow?

Yes, I have put a fair bit of effort into this (5-10 hours sofar), and hitting failure quite a bit more, than I had hoped for, but I am also learning a lot from it, so not everything is lost.
I did manage to isolate massflow, and end up with a calculation in the end, but as another poster have pointed out, I have omitted a lot of key things in my calculations.

 

[Danild]

I think rapid expansions like this are theoretically tough to deal with. I’ve heard @Chestermiller state you shouldn’t ignore viscosity, and there is always speculation about how well the ideal gas assumption works because of the flow being well outside of “passing through equilibrium states”. Also, the flow is unsteady, and the “Energy Equation” is derived under the steady flow assumption. Many things to consider.

Anyhow, are you also ignoring the temperature change?

I was planning to ignore the temperature change at first (so that I got somewhere to begin with), and then add it in later. And yeah, that version of the energy equation I am using is derived under assumption of steady flow, which is why I really started doubting my solution, and I ended up posting it here for some feedback, which turned out to be a good idea. I have probably ended up making a bit too many "optimistic" assumptions it seems.

 

[Danild]

It is so much more complicated than that. You cannot ignore the compressibility effects and cannot assume that velocity won't reach the speed of sound. All of the concepts involved are too complicated to explain simply in this thread. You will also have pressure waves reflected through your cylinder coming back to assist the outflow at the restriction.

I did solve a similar problem in the past - flow through an engine valve between a cylinder and a pipe. Here are the results put graphically for the Mach numbers in the restriction and the pipe:

View attachment 338916​

Where:
$$Ar = \frac{A_{rest}}{A_{pipe}}$$
$$Y = \left(\frac{1}{2.7908k-2.795488}\right)\left(\frac{2X_{pipe\ 0}-1}{X_{cyl}}-1\right)$$
Furthermore:
$$X_n = \left(\frac{p_n}{p_{ref}}\right)^{\frac{k-1}{2k}}$$
$A_n$ is the area of $n$, $k$ is the specific heat ratio (the presented equation for $Y$ is valid for $1.2 \leq k \leq 1.45$), and, in your case, the reference pressure would be the atmospheric pressure which is the "cylinder" pressure as well. ($p_{ref} = p_{cyl} = p_{atm}$)

Your case would represent a positive value for $Y$. A negative value would mean the flow would be from the atmosphere (the "cylinder") to your pipe. The mass flow rate through the restrictor would be:
$$\dot{m} = \rho_{rest}v_{rest}A_{rest} = p_{atm}{X_{rest}}^\frac{k+1}{k-1}\sqrt{\frac{k}{RT_{pipe\ 0}}}M_{rest}A_{rest}$$
$R$ being the specific gas constant and $p_{rest} = p_{cyl}$ (meaning $X_{rest} = 1)$ if $M_{rest} < 1$. If $M_{rest} = 1$ then:
$$X_{rest} = \frac{\frac{2}{k-1} \left(2X_{pipe\ 0}-1\right)}{\frac{2}{k-1} + M_{pipe}} \left(M_{pipe}\frac{A_{pipe}}{A_{rest}}\right)^\frac{k-1}{k+1}$$
This work was done based on the theory found in Design and Simulation of Four-Stroke Engines by Gordon P. Blair.

I'm leaving off the equations for calculating the reflected pressure which would just be too much and useless without a more complex and lengthy context explained.

So assuming the initial conditions $Ar = 0.80$ and $\frac{p_{pipe\ 0}}{p_{ref}} = 4$ (then $Y = 0.394$), you should have a choked flow with $M_{rest} = 1$, $M_{pipe} \approx 0.56$ and $X_{rest} = 1.2186$. (So $p_{rest}$ is basically equal to the pressure in the pipe.)

Edit: I now realize that $Ar = 0.64$ in your case, meaning $M_{pipe} \approx 0.41$ and $X_{rest} = 1.234$.

Thanks for taking the time to post all of that. Though it might take me a little while to decipher it all.
I am getting the impression that I might have been a bit too optimistic about my abilities to calculate this. Maybe I should also check out that book you are mentioning: Do you think it is a good book in terms of understandability?
P.S. I am beginning to realize that this seemingly simple and innocent problem is actually VERY complex to solve by calculation.

 

[jack action]

Do you think it is a good book in terms of understandability?

Sadly, no.