To find the forces on a composite object

[gnits]

Homework Statement

To find the forces on a composite object

Relevant Equations

moments

Could I please ask for help with the following:

Here's a diagram:

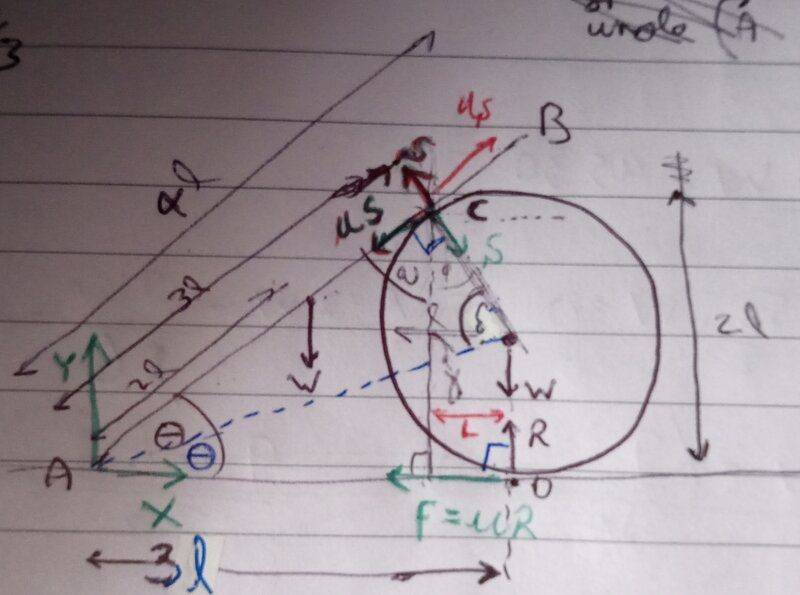
(in what follows, for clarity, I write L to represent the lower case L of the diagram).

My diagram wrongly shows u (the coefficient of friction) to be the same at both points of contact. Since this image was taken I have realized that, it does not affect the following where I refer the coefficient of fruition at C as v.

For the first part of the question the answer in the book is "8W/45 at all points of contact".

I have done that part and agree with the book answer. I obtain F = uR = vS = 8W/45

Intermediate results which I derived and used on the way are that: S = 8w/15 and that R = 23w/15. Also cos(2ɵ)=4/5 and sin(2ɵ)=3/5

For the last part (in this part the coefficient of friction at both points of contact are the same = u) I reasoned that I would balance the horizontal forces acting on the cylinder, like so:

uR + uS*cos(2ɵ) - S*sin(2ɵ)=0

substituting in for S, R, cos(2ɵ) and sin(2ɵ) from above formulae leads to u = 8/49

not 8/21.

Have I made an arithmetic error or have I erroneously applied the wrong physics?

Thanks for any help,
Mitch.

 

[TSny]

Your diagram is a little hard to read. It would be clearer if you drew separate free-body diagrams for the plank and the sphere. I agree with your answers for the normal forces S and R.

You should not assume that a static friction force $f_s$ is always related to the normal force $N$ as $f_s = \mu N$. The correct relation is $f_s \leq \mu N$.

 

[Steve4Physics]

Hi @gnits. I’d like to add a few thoughts...

As @TSny has indicated, the coefficients of friction are not used for the first part of the question. The system is not about to slip. So the coefficient(s) of friction should not appear in the working.
______________

For example, imagine you (weight say 600N) are standing on horizontal ice.

Your friend X applies a horizontal 10N force on you. You do not slide. $F_{friction}$ between you and the ice is therefore 10N as you are still in equilibrium.

X increases the applied force to 20N. You still do not move. $F_{friction}$ has therefore increased to 20N.

X increases the force to 30N. You are now just about to start sliding. (E.g. force of 30.00001N would make you slide). $F_{friction}$ is now 30N and this is the limiting frictional force. The coefficient of static friction is 30/600 = 0,05 and is defined only for this limiting case.
______________

For the second part of the question, note that there are 3 points of contact (point A as well as the 2 contact points on the cylinder).

[I guess that’s why the answer to the first part refers to ‘all’ points of contact. But I think you have considered only 2 – because you used the word ‘both’. So you may still need to find the frictional force at point A.]

There are are various ways sliding could start:
- sliding at point A only;
- sliding at point B only;
- sliding at point O only (I think your diagram shows point ‘O’ at the bottom of the cylinder)’
as well the possibilities of simultaneous sliding at 2 or 3 points of contact.

So I guess you are meant to identify which mode of siding is going to occur first and use that to find μ.

 

[gnits]

Thanks for you detailed answer. I'll get back to it later and let you know how I got on.

 

[gnits]

Well, I'm a little closer to the answer:

Firstly, yes, as Steve4Physics says, A is also a point of contact. And by resolving horizontally on the system as a whole I also get that X = 8w/45. So that completes the first part of the question.

I still believe that my analysis of the cylinder alone, balancing the horizontal forces, which leads to u = 8/49 seems correct. So this would say that, for no slipping at point of contact between cylinder and ground we require u >= 8/49 = 0.163 (to 3 decimal places).

But, taking Steve4Physics' advice made me realize that the rod may slip before the cylinder does. So I balanced the horizontal forces on the rod as follows:

X - S * sin(2ɵ) + u*S * cos(2ɵ) = 0, this leads to u = 1/3. which is greater than 8/49 and so slipping would occur here first, i.e. to not-slip here would require u >= 1/3 = 0.333 (to 3 decimal places) , but this is slightly different to books answer of u >= 8/21 = 0.381 (to 3 decimal places).

I tried balancing vertically for rod only, get same result of u = 1/3.

Would anybody be able to show me where I am reasoning wrongly?

 

[TSny]

If you know the static friction force f and the normal force N at a point of contact, what can you say about the possible values of u at that point of contact?

As a numerical example, suppose f = 2.0 Newtons and N = 8.0 Newtons. What is the range of possible values for u?

Since you know the friction force and the normal force at each of the three contact points in this problem, you can do this type of analysis at each of the points and compare results.

 

[gnits]

Big thanks to both of you for your help. I needed each piece of advice. I get it and agree with the book's answer. Thanks again.