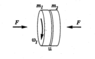- #1
Jenny Physics
- 111
- 4
Homework Statement
A uniform cylindrical wheel of mass ##m_{1}## and radius ##R_{1}## rotates with angular velocity ##\omega_{1}##. It lies a certain distance (along the same axis) from a static wheel of radius ##R_{2}## and mass ##m_{2}##. The wheels are then pushed against each other with a constant force ##F## uniformly distributed across the wheel's face. There is friction ##\mu## between the wheels.
When the wheels first touch what is the magnitude of the torque that wheel 1 exerts on wheel 2 via friction?
Homework Equations
Split wheel 1 into infinitesimal concentric rings of radius ##r## and width ##dr## and find the torque exerted by one of these then integrate to find the total torque.
The Attempt at a Solution
I probably should use ##d\tau=dI \alpha## where ##dI## is the moment of inertia due to the cylindrical ring. But since ##\omega_{1}=const## it would seem that ##\alpha=\dot{\omega}_{1}=0##?