- #1
Jazz
- 103
- 5
I'm confused trying to understand the previous steps that lead to the formula for the angle of an ideally banked curve. In absence of friction, this is the angle where the Centripetal Force is provided by the horizontal component of the Normal Force.
I understand that the Normal Force is perpendicular to the surface where an object is being supported. In an incline, this is the component of the weight that is perpendicular to the slope:
##N = mgcos(\theta) \hspace{20mm} (1)##
And this says the textbook I’m reading :) :
I’ve also drawn the figure but only with the forces (I think the car makes the diagram a little messy):
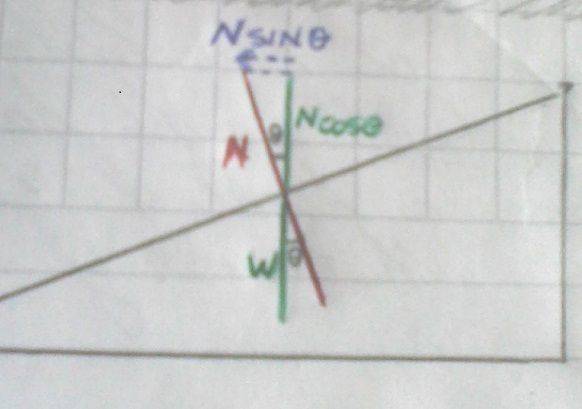
This would mean that I can find ##N## just by dividing both sides by ##cos(\theta)##:
##N = \frac{mg}{cos(\theta)} \hspace{20mm} (2)##
Right from the get go this equation looks quite different from equation ##(1)## (it's like the other way around), and so the results they give should be different.
Probably the following isn't necessary but let suppose there is a car that has a mass of ##5\ kg## in an incline that makes ##30º## with the horizontal. If I try to find ##N## with ##(1)## I get:
##N = mgcos(\theta)##
##N = (5\ kg)(9.8\ m/s)cos(30º)##
##N = 42.2\ N##
Then with ##(2)##:
## N = \frac{mg}{cos(\theta)}##
## N = \frac{(5\ kg)(9.8\ m/s)}{ cos(30º)}##
## N = \frac{(5\ kg)(9.8\ m/s)}{ cos(30º)}##
##N = 56.6\ N##
What am I doing wrong?
It is suppose that the 2nd equation in the quote above is written in terms of ##N## in order to plug it into the other one, rearrange in terms of ##\theta## and finally come up with the formula, but since I cannot make sense of the previous steps I cannot understand the rest of the derivation either.
Thanks!
I understand that the Normal Force is perpendicular to the surface where an object is being supported. In an incline, this is the component of the weight that is perpendicular to the slope:
##N = mgcos(\theta) \hspace{20mm} (1)##
And this says the textbook I’m reading :) :
The figure and the source of this quote is here:Only the normal force has a horizontal component, and so this must equal the centripetal force—that is,
##Nsin(\theta)=\frac{mv^2}{r}##
From the figure, we see that the vertical component of the normal force is ##Ncos(\theta)##, and the only other vertical force is the car’s weight. These must be equal in magnitude; thus,
##Ncos(\theta)=mg##
I’ve also drawn the figure but only with the forces (I think the car makes the diagram a little messy):
This would mean that I can find ##N## just by dividing both sides by ##cos(\theta)##:
##N = \frac{mg}{cos(\theta)} \hspace{20mm} (2)##
Right from the get go this equation looks quite different from equation ##(1)## (it's like the other way around), and so the results they give should be different.
Probably the following isn't necessary but let suppose there is a car that has a mass of ##5\ kg## in an incline that makes ##30º## with the horizontal. If I try to find ##N## with ##(1)## I get:
##N = mgcos(\theta)##
##N = (5\ kg)(9.8\ m/s)cos(30º)##
##N = 42.2\ N##
Then with ##(2)##:
## N = \frac{mg}{cos(\theta)}##
## N = \frac{(5\ kg)(9.8\ m/s)}{ cos(30º)}##
## N = \frac{(5\ kg)(9.8\ m/s)}{ cos(30º)}##
##N = 56.6\ N##
What am I doing wrong?
It is suppose that the 2nd equation in the quote above is written in terms of ##N## in order to plug it into the other one, rearrange in terms of ##\theta## and finally come up with the formula, but since I cannot make sense of the previous steps I cannot understand the rest of the derivation either.
Thanks!
