Twin Paradox with accelerated Motion

[Sagittarius A-Star]

TL;DR Summary

Twin Paradox: Alice with inertial motion, Bob with hyperbolic motion

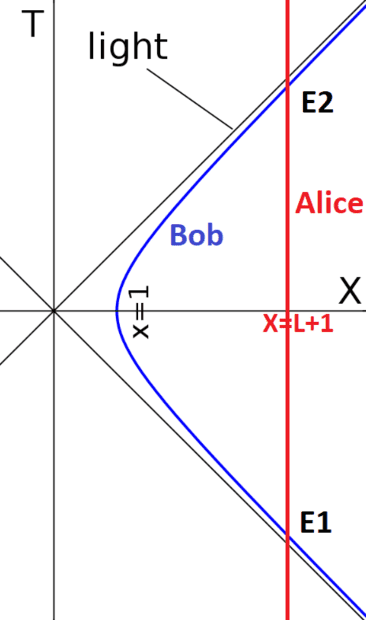
Alice rests at $X=L+1$ in the inertial frame (T, X).
Bob is at rest in the Rindler frame (t, x) at $x=1$ and has the proper acceleration $\alpha=1$.

In the rest frame of Alice, Bob moves from event $E_1=(-T_2, L+1)$ over the distance of $L$ in negative X-direction to event $(0, 1)$ and then returns to event $E_2=(+T_2, L+1)$.

Because of time dilation, Bob's elapsed proper time, when moving form event $(0, 1)$ to event $E_2$, is:
$t_2=\int_0^{T_2} \sqrt{1-\frac{v(T)^2}{c^2}} \ dT \ \ \ \ \ (1)$

Bob's velocity, when moving form event $(0, 1)$ to event $E_2$, is:
$v(T) = \frac{\alpha T}{\sqrt{1+(\alpha T/c)^2}} \ \ \ \ \ (2)$
Source:
https://en.wikipedia.org/wiki/Hyperbolic_motion_(relativity)#Worldline

Plugging equation (2) into equation (1) and setting $c:=1$

$t_2=\int_0^{T_2} \sqrt{1-\frac{\alpha^2 T^2}{1+\alpha^2 T^2}} \, dT =\int_0^{T_2} \sqrt{1-\frac{1}{1+1/(\alpha T)^2}} \, dT \ \ \ \ \ (3)$

Calculating the integral:

$t_2= \frac{\sinh^{-1} {(\alpha T_2)}}{\alpha}= \sinh^{-1} {(T_2)}$

Example $T_2 = 5$:
$t_2=\sinh^{-1} {(5)} \approx 2.31$
For symmetry reasons:
Alice ages by 10 years from event $E_1$ to event $E_2$.
Bob ages by 4.62 years from event $E_1$ to event $E_2$.

 

[PeterDonis]

Nice calculation! Just a couple of comments:

Plugging equation (2) into equation (1) and set $c:=1$

$t_2=T_2\int_0^{T_2} \sqrt{1-\frac{\alpha^2 T^2}{1+\alpha^2 T^2}} \, dT =T_2\int_0^{T_2} \sqrt{1-\frac{1}{1+1/(\alpha T)^2}} \, dT \ \ \ \ \ (3)$

First, there should not be a factor of $T_2$ in front of the integral here (and you drop it later on).

Second, a simpler form for the integral, which matches up more nicely with what you are likely to find online for the derivative of $\sinh^{-1}$, is

$$
\int_0^{T_2} \sqrt{\frac{1}{1 + \alpha^2 T^2}} dT
$$

$t_2= \frac{\sinh^{-1} {(\alpha T_2)}}{\alpha}= \sinh^{-1} {(T_2)}$

With the simpler form for the integral I gave above, evaluating the integral gives

$$
t_2 = \sinh^{-1} \left( \alpha T_2 \right)
$$

Plugging in $\alpha = 1$, which you specified in the problem statement, gives the result you obtain, $t_2 = \sinh^{-1} T_2$.

 

[PeterDonis]

there should not be a factor of $T_2$ in front of the integral here

Source:
https://en.wikipedia.org/wiki/Hyperbolic_motion_(relativity)#Worldline

If you look at the equation for $\tau$ (the proper time of the accelerating object) on this page, you will see that it has a factor $c^2 / \alpha$ in front. I think that is what should be in front of your integral instead of $T_2$ (although there is still a question about the units of the integral itself that I need to think about). Since you have set $\alpha = 1$ (and we could also write $\alpha = c^2 / x$, where $x$ is the Rindler $x$ coordinate of Bob), the final answer comes out the same (in units where $c = 1$).

 

[PeterDonis]

If you look at the equation for (the proper time of the accelerating object) on this page, you will see that it has a factor $c^2 / \alpha$ in front. I think that is what should be in front of your integral

Actually, it doesn't need to be out front of the integral, because it comes out when you evaluate the integral, which I didn't quite do correctly for my version of the integral. Let me do that correctly now by showing more of the steps.

First, let $w = \alpha T$. That means $d w = \alpha d T$, or $dT = dw / \alpha$.

Then we rewrite the integral as follows (in units where $c = 1$):

$$
t_2 = \int_0^{T_2} \sqrt{\frac{1}{1 + \alpha^2 T^2}} dT = \frac{1}{\alpha} \int_0^{\alpha T_2} \sqrt{\frac{1}{1 + w^2}} dw = \frac{1}{\alpha} \sinh^{-1} \left( \alpha T_2 \right)
$$

That now makes the units come out right, since $1 / \alpha$ has units of length (and, as I noted before, it is equal to Bob's Rindler $x$ coordinate). And it also now looks the same as what the OP got from Wolfram Alpha for their version of the integral.

 

[Sagittarius A-Star]

First, there should not be a factor of $T_2$ in front of the integral here (and you drop it later on).

Corrected, thank you!

 

[Orodruin]

This is in essence problem 1.47 from my problem & solutions book. (Although the setting in that problem was described from the instantaneous rest frame of ”Bob” at the first cross of world lines — it is the same problem just posed based on a different frame.)

The solution is more straight forward if you use a parametrization of ”Bob”s world line that uses the hyperbolic sine and cosine, ie,
$$
t = \frac 1a \sinh(u), \quad x = \frac 1a \cosh(u),
$$
which clearly parametrizes the hyperbola $t^2 - x^2 = -1/a^2$. This gives
$$
ds^2 = \frac1{a^2} [\cosh^2(u) - \sinh^2(u)] du^2 = \frac{du^2}{a^2}
$$
making the proper time computation for ”Bob” trivial.

 

[PeterDonis]

Moderator's note: An off topic subthread about the equivalence principle has been deleted. Please keep discussion in this thread focused on the specific analysis presented in the OP.

 

[Sagittarius A-Star]

In the OP, I started the calculation from the general time-dilation formula (1). I wanted to do a plausibility-check, that this formula works also for the special case of a hyperbolic motion of Bob. It was not my intention, to use the "fastest" approach.

Now I repeat the same in the accelerated rest-frame of Bob. The metric in Kottler–Møller coordinates of the Rindler frame with $\tilde{x} = x- \frac{c^2}{\alpha}$ is
$ds^2 = (1+ \frac{\alpha\,\tilde{x}} {c^2})^2c^2dt^2 - (d\tilde{x}^2 + dy^2 + dz^2)$, from which follows the general time-dilation formula, which combines "gravitational" and kinematic time-dilation:$$d\tau = dt\sqrt {(1+ \frac{\alpha\,\tilde{x}} {c^2})^2 - \frac{v^2}{c^2}}$$Bob's proper time is equal to the coordinate-time $t$, because Bob is at rest ($v=0$) at $\tilde{x} = 0$.

Now I calculate the proper time of Alice. To simplify the work of Wolfram Alpha, I set $c:=1$ and re-write this time-dilation formula to Rindler-coordinates:
$d\tau = dt\sqrt {(\alpha\,x)^2 - v^2} = dt\sqrt {x^2 - v^2}$.

Because of time dilation, Alice's elapsed proper time, when moving form event (0, L+1) to event E2, is:
$T_2=\int_0^{t_2} \sqrt{x(t)^2-v(t)^2} \ dt \ \ \ \ \ (1)$

Alice's velocity, when moving form event (0, L+1) to event E2, is:
Edited:
$v(t) = -\tanh {(t)} x(t)\ \ \ \ \ (2)$
Source:
https://en.wikipedia.org/wiki/Hyperbolic_motion_(relativity)#Worldline
Edited: I multiplied with $x(t)$, because also the velocity is effected by "gravitational" time dilation.

Alice's x-coordinate, when moving form event (0, L+1) to event E2, is:
$x(t) = \sqrt{X^2-T(t)^2} = \sqrt{(L+1)^2-[(L+1) \tanh{(t)}]^2} = \sqrt{(\frac{T_2}{\tanh{(t_2)}})^2-[\frac{T_2 \tanh{(t)}}{\tanh{(t_2)}}]^2 }$
$=\frac{T_2}{\tanh{(t_2)}} \sqrt{1-\tanh^2{(t)}} \ \ \ \ \ (3)$
Source:
https://en.wikipedia.org/wiki/Rindler_coordinates#Variants_of_transformation_formulas

Plugging equations (2) and (3) into (1):

$T_2=\frac{T_2}{\tanh{(t_2)}} \int_0^{t_2} (1- \tanh^2{(t)})\ dt =\frac{T_2}{\tanh{(t_2)}} \tanh{(t_2)} = T_2 \ \ \ \ \ (4)$
Source:
https://www.wolframalpha.com/input?i2d=true&i=Integrate[\(40)1-Power[tanh\(40)t\(41),2],t]

That does not look wrong

 

[DrGreg]

I haven't checked the rest of your working, but in the Wikipedia article $v$ is $\tanh\tau$, not $\tanh t$.

 

[PeterDonis]

Does someone find the error(s)?

You can't assume that $v$ in Rindler coordinates is the same as $v$ in Minkowski coordinates.

 

[Sagittarius A-Star]

I haven't checked the rest of your working, but in the Wikipedia article $v$ is $\tanh\tau$, not $\tanh t$.

I think, with $\tau$ they mean in Wikipedia the proper time of Bob. In the accelerated rest frame of Bob that is equal to $t$, because Bob is at rest at $x=1$ and $\alpha := 1$.

 

[Sagittarius A-Star]

You can't assume that $v$ in Rindler coordinates is the same as $v$ in Minkowski coordinates.

Yes, that was the error. I corrected it by multiplying the original term for $v$ with $\alpha x(t)$, because also the velocity is effected by "gravitational" time dilation.
Thank you!

 

[Sagittarius A-Star]

By the way, are you sure that whoever is in the spaceship, that goes pass Earth at quasi c-speed is Bob? Or, if it's Bob, what age it has when it passes along Earth in such a hurry? Because the only thing you prove is that the astronaut ages 2.31 years, but not how many years its has to begin with.

I assume, that Bob has the same age as Alice, when Bob passes first time the earth.

And the boarding and unboarding is a little questionable

To make the calculation easier, boarding and unboarding were canceled

 

[Sagittarius A-Star]

I think that what you need is:
$d\tau=(1+\frac{g \cdot x'}{c^2})\,dt'$

There the kinematic part of the time-dilation of Alice is missing, because Alice is moving in Bob's accelerated rest-frame.

 

[pervect]

Baez's synopsis of the "relativistic rocket" equation from the old sci.physics FAQ confirms the result using Sagittarius' notation that with a=c=1, $t_2 = \sinh ^ {-1} T_2$

Baez's webpage with the FAQ is at https://math.ucr.edu/home/baez/physics/Relativity/SR/Rocket/rocket.html.

Note that (X,T) in Sagittarius analysis is (x,t) in Baez's notation, and in Baez's notation, Bob's proper time is given by T.

The full equation, with units is, in Baez's notation is

$$T = \frac{c}{a} \sinh^{-1} \frac{at}{c}$$

Changing to Sagittarius' notation this becomes
$$\tau = t_2 = \frac{c}{a} \sinh^{-1} \frac{aT_2}{c}$$

Hi,

I think that what you need is:

$d\tau=(1+\frac{g \cdot x'}{c^2})\,dt'$

...

No, this is incorrect as others have noted.

Using Llluis' slightly different notation (which adds a prime) one needs to solve for $d\tau$ from the relationship

$$c^2 d\tau^2 = c^2 \, \left( 1+ \frac{g x'}{c^2} \right)^2 \, dt'^2 - dx'^2$$

In Bob's accelerated frame, Alice's dx' is not zero.

 

[Sagittarius A-Star]

Changing to Sagittarius' notation this becomes
$$\tau = t_2 = \frac{c}{a} \sinh^{-1} \frac{aT_2}{c}$$

This formula is also valid for $\frac{1}{4}$ of Bob's overall elapsed proper time in Llluis' scenario, with $T_2=\frac{20}{4}\ \text{years}$ .