- #1
- 1,301
- 976
- TL;DR Summary
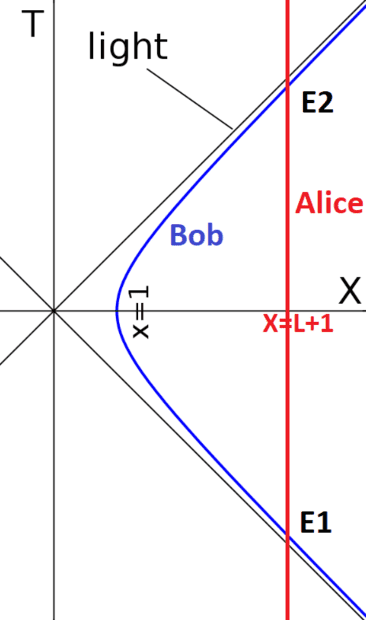
- Twin Paradox: Alice with inertial motion, Bob with hyperbolic motion
Alice rests at ##X=L+1## in the inertial frame (T, X).
Bob is at rest in the Rindler frame (t, x) at ##x=1## and has the proper acceleration ##\alpha=1##.
In the rest frame of Alice, Bob moves from event ##E_1=(-T_2, L+1)## over the distance of ##L## in negative X-direction to event ##(0, 1)## and then returns to event ##E_2=(+T_2, L+1)##.
Because of time dilation, Bob's elapsed proper time, when moving form event ##(0, 1)## to event ##E_2##, is:
##t_2=\int_0^{T_2} \sqrt{1-\frac{v(T)^2}{c^2}} \ dT \ \ \ \ \ (1)##
Bob's velocity, when moving form event ##(0, 1)## to event ##E_2##, is:
##v(T) = \frac{\alpha T}{\sqrt{1+(\alpha T/c)^2}} \ \ \ \ \ (2)##
Source:
https://en.wikipedia.org/wiki/Hyperbolic_motion_(relativity)#Worldline
Plugging equation (2) into equation (1) and setting ##c:=1##
##t_2=\int_0^{T_2} \sqrt{1-\frac{\alpha^2 T^2}{1+\alpha^2 T^2}} \, dT =\int_0^{T_2} \sqrt{1-\frac{1}{1+1/(\alpha T)^2}} \, dT \ \ \ \ \ (3)##
Calculating the integral:
##t_2= \frac{\sinh^{-1} {(\alpha T_2)}}{\alpha}= \sinh^{-1} {(T_2)} ##
Example ##T_2 = 5##:
##t_2=\sinh^{-1} {(5)} \approx 2.31##
For symmetry reasons:
Alice ages by 10 years from event ##E_1## to event ##E_2##.
Bob ages by 4.62 years from event ##E_1## to event ##E_2##.
Bob is at rest in the Rindler frame (t, x) at ##x=1## and has the proper acceleration ##\alpha=1##.
In the rest frame of Alice, Bob moves from event ##E_1=(-T_2, L+1)## over the distance of ##L## in negative X-direction to event ##(0, 1)## and then returns to event ##E_2=(+T_2, L+1)##.
Because of time dilation, Bob's elapsed proper time, when moving form event ##(0, 1)## to event ##E_2##, is:
##t_2=\int_0^{T_2} \sqrt{1-\frac{v(T)^2}{c^2}} \ dT \ \ \ \ \ (1)##
Bob's velocity, when moving form event ##(0, 1)## to event ##E_2##, is:
##v(T) = \frac{\alpha T}{\sqrt{1+(\alpha T/c)^2}} \ \ \ \ \ (2)##
Source:
https://en.wikipedia.org/wiki/Hyperbolic_motion_(relativity)#Worldline
Plugging equation (2) into equation (1) and setting ##c:=1##
##t_2=\int_0^{T_2} \sqrt{1-\frac{\alpha^2 T^2}{1+\alpha^2 T^2}} \, dT =\int_0^{T_2} \sqrt{1-\frac{1}{1+1/(\alpha T)^2}} \, dT \ \ \ \ \ (3)##
Calculating the integral:
##t_2= \frac{\sinh^{-1} {(\alpha T_2)}}{\alpha}= \sinh^{-1} {(T_2)} ##
Example ##T_2 = 5##:
##t_2=\sinh^{-1} {(5)} \approx 2.31##
For symmetry reasons:
Alice ages by 10 years from event ##E_1## to event ##E_2##.
Bob ages by 4.62 years from event ##E_1## to event ##E_2##.
Last edited: