Two Blocks, a Pulley and an Inclined Plane

[rudransh verma]

Homework Statement

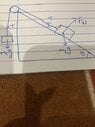
A 55 g mass is attached to a light string, which is placed over a frictionless, massless pulley, and attached to a 199 gm block which is on a board inclined at 39.3° as shown. Assuming the block starts at rest and the $\mu_k$ between
the incline and block is 0.38, how long will it take the block to move 13 cm?

Relevant Equations

$F_Net=ma$

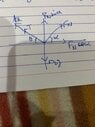
1. $-f_k\cos\theta-T\cos\theta+F_n\cos\alpha=m_2a_x$
2. $f_k\sin\theta+T\sin\theta+F_n\sin\alpha-m_2g=-m_2a_y$
3. $T-m_1g=m_1a_y$

I am unable to get anywhere. There are accelerations in x , y directions.
I need the value of acceleration. Then I can simply use $s=ut+\frac12at^2$

 

[kuruman]

The magnitude of the acceleration is the same for both blocks because the connecting string does not stretch or shrink. It's OK to have differently oriented axes for separate FBDs. The one for the hanging mass is fine. For the mass on the incline, orient the axes to be parallel and perpendicular to the incline. That should make the equations simpler to write down and manipulate because the component of the acceleration perpendicular to the incline in the second FBD is zero.

 

[rudransh verma]

The magnitude of the acceleration is the same for both blocks because the connecting string does not stretch or shrink. It's OK to have differently oriented axes for separate FBDs. The one for the hanging mass is fine. For the mass on the incline, orient the axes to be parallel and perpendicular to the incline. That should make the equations simpler to write down and manipulate because the component of the acceleration perpendicular to the incline in the second FBD is zero.

Ok! Are these eqns unsolvable? First help me with these ones then I will try your way too.

 

[kuruman]

Ok! Are these eqns unsolvable? First help me with these ones then I will try your way too.

They are not unsolvable but you don't have enough of them and the ones you have are not error-free. You have not included the constraint that the magnitude of the acceleration is the same for both blocks and what you have for the acceleration components is incorrect. In your equations (2) and (3) you assign to the vertical components of the acceleration of $m_1$ and $m_2$ the same symbol $a_y$. That means that the magnitude of the acceleration of $m_1$ is $a_y$ while the magnitude of the acceleration for $m_2$ is $\sqrt{a_x^2+a_y^2}$. Unless the horizontal acceleration for $m_2$ is zero (which it isn't) the magnitudes are not equal. Furthermore, you are making your task even more difficult by introducing angle $\alpha$. As I indicated in the other thread of the person standing on the incline, doing something like this raises barriers rather than facilitate algebraic manipulation.

The widely used advice for FBDs is "Orient your coordinate axes so that the acceleration is along one of the principal axes." This is excellent advice because when you write Newton's 2nd law, the right-hand side of one equation is zero. You can do that because the accelerating mass doesn't know or care which way you chose to orient your axes. It will accelerate just the same. Try my way, actually the widely recommended way, first and then try the horizontal-vertical orientation for the incline FBD if you have a penchant for unnecessary and tedious work. I do not.

 

[Steve4Physics]

@rudransh verma, it is not 100% clear to me (without doing calculations) which direction the block on the slope will slide on release – uphill or downhill? You might want to check this.

 

[rudransh verma]

The widely used advice for FBDs is "Orient your coordinate axes so that the acceleration is along one of the principal axes." This is excellent advice because when you write Newton's 2nd law, the right-hand side of one equation is zero. You can do that because the accelerating mass doesn't know or care which way you

I got it. t= 0.733 secs. Thanks. It has become so easy like this.

 

[kuruman]

I got it. t= 0.733 secs. Thanks. It has become so easy like this.

That's the number I got. Congratulations.

 

[kuruman]

@rudransh verma :
@Steve4Physics's comment in post #5 is very important. Before you start a problem like this one, you need to figure out which way the system will slide: is the hanging mass ascending or descending. It could be either way depending on the ratio of the masses and the angle of the incline. Which way the system will move is important for determining whether the force of friction points up or down the incline. You can find that direction by figuring out the direction of the acceleration when the incline is frictionless. The acceleration will not change sign if the incline becomes rough. In this problem you had a 50-50 chance to choose correctly and you did. That may not be the case next time you encounter a problem like this.

 

[rudransh verma]

Unless the horizontal acceleration for m2 is zero (which it isn't) the magnitudes are not equal.

It is true that the acceleration magnitude should be equal for masses. But it’s also true that there is horizontal component of a in standard axis orientation. So how will both be equal because it’s not wrong to orient that way. Can you show just for knowledge?

In this problem you had a 50-50 chance to choose correctly and you did. That may not be the case next time you encounter a problem like this.

First of all there is no question that heavier mass will take lighter ones with it. In frictionless situation both should fall at same rate.
Previously I thought and solved problems using heavier mass will pull the lighter ones but this is not true.
So yes I don’t know which way will it fall

 

[kuruman]

It is true that the acceleration magnitude should be equal for masses. But it’s also true that there is horizontal component of a in standard axis orientation. So how will both be equal because it’s not wrong to orient that way. Can you show just for knowledge?

They cannot be equal and I did not say that they are. You said that in equations (2) and (3), post #1.

2. $f_k\sin\theta+T\sin\theta+F_n\sin\alpha-m_2g=-m_2a_y$
3. $T-m_1g=m_1a_y$

In equation (3) the right hand side has $a_y$ for the vertical component of the acceleration of $m_1$. Here the acceleration vector is in the vertical direction, so the magnitude of the vertical component is the same as the magnitude of the vector.

In equation (2) the right hand side has also $a_y$ for the vertical component of the acceleration of $m_2$. Here the acceleration vector is not in the vertical direction and the magnitude of the vertical component cannot be the same as the magnitude of the vector. So equations (3) and (2) are inconsistent because they require two different values for the same variable.

On edit: The segment above has been edited to correct a mixup of equations and masses as pointed out by OP in post #11. Also see retraction in Post #13.

First of all there is no question that heavier mass will take lighter ones with it. In frictionless situation both should fall at same rate.

There is a question. It is not always true that "the heavier mass will take the lighter ones with with it." If the angle of the incline is zero (horizontal plane) the hanging mass will descend no matter how heavy the mass on the horizontal plane is. Now imagine changing the angle slowly so that the angle of the plane increases above the horizontal. There will be a critical angle at which the acceleration will go to zero. If you increase the angle beyond that value, only then the acceleration will change direction and "the heavier mass will take the lighter one with with it."

Don't guess - calculate.

 

[rudransh verma]

Here the acceleration vector is in the vertical direction, so the magnitude of the vertical component is the same as the magnitude of the vector.

But its not. Acceleration vector is in forth quadrant in the xy plane. It has both horizontal and vertical components. To be clear I am talking about my original way of orienting the xy plane.

In equation (3) the right hand side has also ay for the vertical component of the acceleration of m2.

of m1?

 

[rudransh verma]

Don't guess - calculate.

Well I calculated and got a=-4.996 m/s^2.
And time $t=\sqrt{-something}$.
So that’s why the acceleration of 199 gms is downwards and not upwards ? My assumption is wrong?

 

[kuruman]

But its not. Acceleration vector is in forth quadrant in the xy plane. It has both horizontal and vertical components. To be clear I am talking about my original way of orienting the xy plane.

of m1?

You are correct in being puzzled. I inadvertently mixed up equations and masses. I edited post #10 to what it should have been. The fact remains that if the mass hanging straight down has y-component of the acceleration equal to $a_y$, the y-component of the acceleration of the mass sliding on the plane cannot also be $a_y$. I thank you for pointing this out and I apologize for the confusion it might have caused.

Well I calculated and got a=-4.996 m/s^2.
And time $t=\sqrt{-something}$.
So that’s why the acceleration of 199 gms is downwards and not upwards ? My assumption is wrong?

Please show me the equations that you used. Remember, every time you want to know why there is something wrong in your calculations, you need to show what you did. If $a$ stands for the magnitude of the acceleration, it should come out positive after you put in the numbers. If it comes out negative, this means that one or more of the following is true
1. You assumed that the direction of the acceleration vector is in the opposite direction of what it ought to be but its magnitude is correct.
2. You drew one or more forces incorrectly in your FBDs.
3. You wrote one or more Newton's second law equations inconsistently with the FBDs.

I cannot figure out which is the case here unless you provide me with the information.

 

[jbriggs444]

@rudransh verma :
@Steve4Physics's comment in post #5 is very important. Before you start a problem like this one, you need to figure out which way the system will slide: is the hanging mass ascending or descending. It could be either way depending on the ratio of the masses and the angle of the incline. Which way the system will move is important for determining whether the force of friction points up or down the incline. You can find that direction by figuring out the direction of the acceleration when the incline is frictionless. The acceleration will not change sign if the incline becomes rough. In this problem you had a 50-50 chance to choose correctly and you did. That may not be the case next time you encounter a problem like this.

If it is not obvious which way the system will move, you can figure it out the hard way (as @kuruman knows well).

Make an assumption that it moves a particular way [or stays stationary]. This determines which way kinetic friction will act [or whether static friction is at work].

Solve the system to decide how fast it accelerates [or how much static friction you need].

If the direction of the acceleration is opposite to your assumption, then your assumption was wrong.

If the force of static friction exceeds the maximum dictated by $\mu_s$ then your assumption that the system was stationary was wrong.

If your assumption was wrong, make a different one. It should turn out that at least one of the three possible assumptions is viable. It is sometimes possible for two of them to be viable.

 

[rudransh verma]

So equations (3) and (2) are inconsistent because they require two different values for the same variable.

How? The body hanging and the body on the slide should equally accelerate in vertical direction. It is because there is ax too for the sliding body it doesn’t move actually in vertical direction like the hanging body.

 

[rudransh verma]

If the direction of the acceleration is opposite to your assumption, then your assumption was wrong.

My assumption was that the hanging mass should go downwards and my acceleration did come -ve.
So I am right?

 

[Lnewqban]

How? The body hanging and the body on the slide should equally accelerate in vertical direction. It is because there is ax too for the sliding body it doesn’t move actually in vertical direction like the hanging body.

If you cut the rope, how much the block on the slide would accelerate in the vertical direction only?

 

[kuruman]

If the direction of the acceleration is opposite to your assumption, then your assumption was wrong.

That is true. However, if the acceleration comes out positive (according to your expectation) this does not necessarily mean that the calculation is correct. In this particular problem, one can do two calculations:
1. Assume that the mass on the incline slides down and take "down incline" as positive which means that "up" is positive for the ascending mass.
2. Assume that the mass on the incline slides up and take "up incline" as positive which means that "down" is positive for the descending mass.

Upon substitution, the first calculation gives a positive numerical answer and the correct magnitude.
Upon substitution, the second calculation gives a negative numerical answer with magnitude different from the previous value.

Finding the direction of motion is crucial for determining whether the kinetic friction is parallel to the tension (case 1) or antiparallel (case 2) because that affects the magnitude of the acceleration, not only the sign.

 

[rudransh verma]

Assume that the mass on the incline slides up and take "up incline" as positive which means that "down" is positive for the descending mass.

I took down incline as positive and up vertical as positive. I assumed the mass goes up the incline and the hanging mass go down. When calculated I got -acceleration. So what does it mean?

 

[rudransh verma]

If you cut the rope, how much the block on the slide would accelerate in the vertical direction only?

$a_y=\sqrt{a^2-a_x^2}$
But the hanging mass moves $a_y=a$

 

[kuruman]

I took down incline as positive and up vertical as positive. I assumed the mass goes up the incline and the hanging mass go down. When calculated I got -acceleration. So what does it mean?

The first assumption is OK. You can either makes this choice or up incline as positive and down vertical as positive. These are consistent. You do not have the freedom to assume the direction in which the masses move. If you are not told, you have to figure that out. See post #8. Anyway, I thought we had already agreed that $m_2$ moves down the incline. Why did you change your mind?

 

[Lnewqban]

$a_y=\sqrt{a^2-a_x^2}$
But the hanging mass moves $a_y=a$

But, we don't know a or a aligned with your x-axis for the block alone (we have cut the string) that is sliding down the incline.
Where is gravity there?
Where is the angle of the slope?
Can you produce an equation for vertical acceleration that includes parameters that we know?

 

[rudransh verma]

The first assumption is OK. You can either makes this choice or up incline as positive and down vertical as positive. These are consistent. You do not have the freedom to assume the direction in which the masses move. If you are not told, you have to figure that out. See post #8. Anyway, I thought we had already agreed that $m_2$ moves down the incline. Why did you change your mind?

I am trying to understand to figure out which way the masses will accelerate. So that’s why I assumed the mass inclined on the plane moves up and so look at the result to determine the direction of motion.
So when I did that I got negative acceleration. So I ask you now how does it justify that my assumption was wrong that the mass moves up the plane.

 

[rudransh verma]

an you produce an equation for vertical acceleration that includes parameters that we know?

Why? I just want to know how the vertical accelerations of the bodies are different so that my eqns in OP are wrong which they are.

 

[vela]

If it comes out negative, this means that one or more of the following is true
1. You assumed that the direction of the acceleration vector is in the opposite direction of what it ought to be but its magnitude is correct.
2. You drew one or more forces incorrectly in your FBDs.
3. You wrote one or more Newton's second law equations inconsistently with the FBDs.

4. You screwed up the algebra. (I find this to be my most common mistake.)

 

[Lnewqban]

Why? I just want to know how the vertical accelerations of the bodies are different so that my eqns in OP are wrong which they are.

Why not?
I just want you to see how, based on both systems of coordinates being horizontal-vertical, as you wanted them to be.

 

[rudransh verma]

Why not?
I just want you to see how, based on both systems of coordinates being horizontal-vertical, as you wanted them to be.

Edit: Ok!
$\frac{F_n\sin⁡α−m_2g}{m_2}=-a_1y$
$\frac{m_1g}{m_1}=a_2y=g$
I removed friction to simplify

 

[Steve4Physics]

I am trying to understand to figure out which way the masses will accelerate. So that’s why I assumed the mass inclined on the plane moves up and so look at the result to determine the direction of motion.

If you want to know which way the masses accelerate, just compare the two competing ‘driving’ forces and see which is biggest:
- the weight of mass-1: $m_1g$ vertically downwards;
- the downhill component of the weight of mass-2: $m_2gsin θ$ downhill to the right

Of course, you only really need to compare $m_1$ and $m_2sinθ$ as the ‘g’s cancel.

A few seconds on your calculator does the trick.

I I think I already explained this in another thread.

 

[rudransh verma]

you want to know which way the masses accelerate, just compare the two competing ‘driving’ forces and see which is biggest:
- the weight of mass-1: m1g vertically downwards;
- the downhill component of the weight of mass-2: m2gsinθ downhill to the right

What about assuming a particular direction and deciding by the value we get after calculation?
That’s what you said in some previous post.

 

[kuruman]

What about assuming a particular direction and deciding by the value we get after calculation?
That’s what you said in some previous post.

That by itself will not do it. To get the correct magnitude of the acceleration, you also need to know which way the system will accelerate if friction is turned off and take that to be the direction of the acceleration when the masses are released from rest and the incline is rough. I explained all that in post #18. Please read it.

 

[vela]

Ok!
$\frac{F_n\sin⁡α−m_2g}{m_2}=-ay$
$\frac{m_1g}{m_1}=ay=g$
I removed friction to simplify

One problem I've seen in multiple threads now is that you don't carefully define your variables. According to the equations you wrote down, mass 1 accelerates at 9.81 m/s^2. Is that what you really meant?

You have $\vec a_1$, the acceleration of mass 1, and its components $a_{1x}$ and $a_{1y}$. Same goes for mass 2. Try rewriting your equations carefully in terms of these variables. Then figure out which ones are zero, which components are equal, etc. Be able to justify everything.

 

[Lnewqban]

This is hopelessly incorrect. You not only removed friction, but you also removed the tension which says that the mass is in free fall. Also, the vertical component of the acceleration for the mass on the incline does not have the same magnitude as the vertical component of the acceleration of the hanging mass. You cannot give them the same name.

OP has produced those equations excluding the string tension as a response my question in post #17.
Just trying to make him understand about the vertical acceleration of m2.

 

[rudransh verma]

Just trying to make him understand about the vertical acceleration of m2.

So am I correct?

 

[kuruman]

OP has produced those equations excluding the string tension as a response my question in post #17.
Just trying to make him understand about the vertical acceleration of m2.

I see. I misunderstood what OP was doing. I deleted my post to keep distractions to a minimum.

 

[Steve4Physics]

What about assuming a particular direction and deciding by the value we get after calculation?
That’s what you said in some previous post.

Assuming a particular direction might work for some problems (e.g. zero friction). Maybe that's what you are referring to by 'some previous post'?

But I have definitely not said it in the context of this current thread. In Post #5 I simply suggested that you might want to check the direction. @kuruman explained the reason in Post#8.

Ignoring units: $m_1=55$ and $m_2sinθ= 199sin(39.3°) =126$.
Since 126>55 we now know mass-2 moves downhill.
It took only a moment to find out!